题目内容
【题目】如图,△ABC中,AB=AC,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=26°,E、F分别是BC、AC的中点,则∠EDF等于 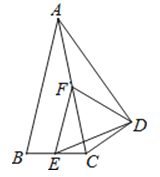
【答案】![]()
【解析】解:∵E、F分别是BC、AC的中点,∠CAD=∠CAB=26°,
∴EF是△ABC的中位线,
∴EF=![]() AB,∠EFC=∠CAB=26°.
AB,∠EFC=∠CAB=26°.
∵AB=AC,△ACD是直角三角形,点E是斜边AC的中点,
∴DF=AF=CF,
∴DF=EF,∠CAD=∠ADF=26°.
∵∠DFC是△AFD的外角,
∴∠DFC=26°+26°=52°,
∴∠EFD=∠EFC+∠DFC=26°+52°=78°,
∴∠EDF=![]() =51°.
=51°.
故答案为:![]() .
.
先根据题意判断出△DEF的形状,由平行线的性质得出∠EFC的度数,再由三角形外角的性质求出∠DFC的度数,再根据三角形内角和定理即可得出结论.

练习册系列答案
相关题目
