题目内容
(2004•湖州)已知如图,直线y=-2x+2与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作等腰直角△ABC,∠BAC=90°,过C作CD⊥x轴,垂足为D.(1)求点A、B的坐标和AD的长;
(2)求过B、A、D三点的抛物线的解析式.
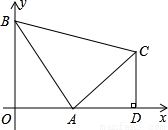
【答案】分析:(1)已知了直线AB的解析式,令解析式的y=0,可得出A点的坐标.令x=0,可得出B点的坐标.由于∠BAC=90°且AB=AC,可证得△AOB≌△COA,由此可得出OB=AD,OA=CD,由此可求出AD的长;
(2)在(1)中不难得出D点的坐标,然后根据A、B、D三点坐标,用待定系数法即可求出抛物线的解析式.
解答:解:(1)对于直线y=-2x+2,
令x=0,求得y=2,即B(0,2);令y=0,求得x=1,即A(1,0),
∵∠BAC=90°,
∴∠ABO=∠CAD=90°-∠OAB,
在△ABO和△CAD中,
 ,
,
∴△ABO≌△CAD(AAS),
∴AD=BO=2;
(2)设经过A、B、D三点的抛物线的解析式为y=a(x-m)(x-n)
由(1)可得:D点坐标为(3,0),又A(1,0),B(0,2)
∴ ,
,
解得: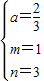 ,
,
∴所求解析式为y= (x-1)(x-3)
(x-1)(x-3)
即y= x2-
x2- x+2.
x+2.
点评:本题考查了等腰直角三角形的性质、全等三角形的判定和性质、二次函数解析式的确定等知识.
(2)在(1)中不难得出D点的坐标,然后根据A、B、D三点坐标,用待定系数法即可求出抛物线的解析式.
解答:解:(1)对于直线y=-2x+2,
令x=0,求得y=2,即B(0,2);令y=0,求得x=1,即A(1,0),
∵∠BAC=90°,
∴∠ABO=∠CAD=90°-∠OAB,
在△ABO和△CAD中,
 ,
,∴△ABO≌△CAD(AAS),
∴AD=BO=2;
(2)设经过A、B、D三点的抛物线的解析式为y=a(x-m)(x-n)
由(1)可得:D点坐标为(3,0),又A(1,0),B(0,2)
∴
 ,
,解得:
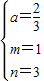 ,
,∴所求解析式为y=
 (x-1)(x-3)
(x-1)(x-3)即y=
 x2-
x2- x+2.
x+2.点评:本题考查了等腰直角三角形的性质、全等三角形的判定和性质、二次函数解析式的确定等知识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 经过点A(2,-3),则k的值是 .
经过点A(2,-3),则k的值是 . 经过点A(2,-3),则k的值是 .
经过点A(2,-3),则k的值是 . 经过点A(2,-3),则k的值是 .
经过点A(2,-3),则k的值是 . 经过点A(2,-3),则k的值是 .
经过点A(2,-3),则k的值是 . 经过点A(2,-3),则k的值是 .
经过点A(2,-3),则k的值是 .