题目内容
已知△ABC的两条高线的长分别为5和20,若第三条高线的长也是整数,则第三条高线长的最大值为
- A.5
- B.6
- C.7
- D.8
B
分析:如果设△ABC的面积为S,所求的第三条高线的长为h,根据三角形的面积公式,先用含S、h的代数式分别表示出三边的长度,再由三角形三边关系定理,列出不等式组,求出不等式组的解集,得到h的取值范围,然后根据h为整数,确定h的值.
解答:设△ABC的面积为S,所求的第三条高线的长为h,则三边长分别为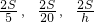 ,则
,则 .
.
由三边关系,得 ,
,
解得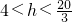 .
.
所以h的最大整数值为6,即第三条高线的长的最大值为6.
故选B.
点评:本题主要考查了三角形的面积公式,三角形三边关系定理及不等式组的解法,有一定难度.利用三角形的面积公式,表示出△ABC三边的长度,从而运用三角形三边关系定理,列出不等式组是解题的关键,难点是解不等式组.
分析:如果设△ABC的面积为S,所求的第三条高线的长为h,根据三角形的面积公式,先用含S、h的代数式分别表示出三边的长度,再由三角形三边关系定理,列出不等式组,求出不等式组的解集,得到h的取值范围,然后根据h为整数,确定h的值.
解答:设△ABC的面积为S,所求的第三条高线的长为h,则三边长分别为
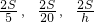 ,则
,则 .
.由三边关系,得
 ,
,解得
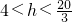 .
.所以h的最大整数值为6,即第三条高线的长的最大值为6.
故选B.
点评:本题主要考查了三角形的面积公式,三角形三边关系定理及不等式组的解法,有一定难度.利用三角形的面积公式,表示出△ABC三边的长度,从而运用三角形三边关系定理,列出不等式组是解题的关键,难点是解不等式组.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
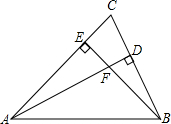
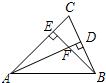 1、如图,已知△ABC的两条高AD、BE交于F,AE=BE,
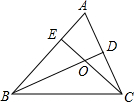
1、如图,已知△ABC的两条高AD、BE交于F,AE=BE, 如图,已知△ABC的两条高线BD、CE相交于点O,且BE=EC.求证:BO=AC.
如图,已知△ABC的两条高线BD、CE相交于点O,且BE=EC.求证:BO=AC.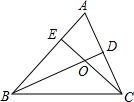 已知△ABC的两条高BD与CE相交于点O,且∠BOC=125°,求∠A的度数.
已知△ABC的两条高BD与CE相交于点O,且∠BOC=125°,求∠A的度数.