题目内容
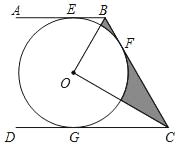
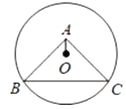
【题目】如图，
过点B、C，圆心O在等腰
的内部，
，
，
．则的半径为（ ）
A.5B.
C.
D.
【答案】A
【解析】
过O作OD⊥BC，由垂径定理可知BD=CD=
BC，根据△ABC是等腰直角三角形可知∠ABC=45°，故△ABD也是等腰直角三角形，BD=AD，再由OA=1可求出OD的长，在Rt△OBD中利用勾股定理即可求出OB的长．
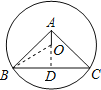
解：过O作OD⊥BC，
∵BC是⊙O的一条弦，且BC=8，
∴BD=CD=
，
∴OD垂直平分BC，又AB=AC，
∴点A在BC的垂直平分线上，即A，O及D三点共线，
∵△ABC是等腰直角三角形，
∴∠ABC=45°，
∴△ABD也是等腰直角三角形，
∴AD=BD=4，
∵OA=1，
∴OD=AD-OA=4-1=3，
在Rt△OBD中，
OB=
．
故答案为：A．
练习册系列答案
相关题目
【题目】某校学生会为了解本校学生每天体育锻炼所用时间情况，采用问卷的方式对一部分学生进行调查确定调查对象时，大家提出以下几种方案：（A）对各班体育委员进行调査；（B）对某班的全体学生进行调查；（C）从全校每班随机抽5名学生进行调查在问卷调查时，每位被调查的学都选择了问卷中适合自己的十个时间段，学生会将收集到的数据整理后续制成如下的统计表：
被调查的学生每天体育锻炼所用时间统计表
组别 | 时间x（小时） | 频数 |
一 | 0≤x≤0.5 | 15 |
二 | 0.6＜x≤1 | 27 |
三 | 1＜x≤1.5 | 38 |
四 | 1.5＜x≤2 | 13 |
五 | x＞2 | 7 |
（1）为了使收集到的数据具有代表性，学生会在确定调查对象时选择了方案 （填A、B或C）；
（2）被调查的学生每天体育锻炼所用时间的中位数落在 组；
（3）根据以上统计结果，估计该校900名学生中每天体育锻炼时间不超过0.5小时的人数，并根据你计算的结果提出一条合理化建议．