题目内容
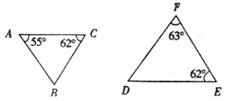
 如图的两个三角形是否相似,为什么?若相似,写出对应边.
如图的两个三角形是否相似,为什么?若相似,写出对应边.
解:∵∠B=180°-∠A-∠C,∠D=180°-∠E-∠F,
∴∠B=63°,∠D=55°,
∴∠A=∠D,∠C=∠E,∠B=∠F,
∴△ABC∽△DFE;
且对应边分别为:AB对应DF,BC对应FE,CA对应ED.
分析:根据三角形内角和定理,即可求得∠B、∠D的度数,根据对应角相等的性质即可求证△ABC∽△DFE,写出对应边即可解题.
点评:本题考查了三角形内角和定理,考查了相似三角形的证明,考查了相似三角形对应边比值相等的性质,本题中求∠B、∠D的度数是解题的关键.
∴∠B=63°,∠D=55°,
∴∠A=∠D,∠C=∠E,∠B=∠F,
∴△ABC∽△DFE;
且对应边分别为:AB对应DF,BC对应FE,CA对应ED.
分析:根据三角形内角和定理,即可求得∠B、∠D的度数,根据对应角相等的性质即可求证△ABC∽△DFE,写出对应边即可解题.
点评:本题考查了三角形内角和定理,考查了相似三角形的证明,考查了相似三角形对应边比值相等的性质,本题中求∠B、∠D的度数是解题的关键.

练习册系列答案
相关题目

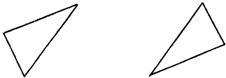 37、如图所示的两个三角形是否成中心对称?若是,请画出对称中心.
37、如图所示的两个三角形是否成中心对称?若是,请画出对称中心.