题目内容
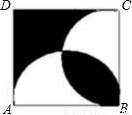
如图，分别以正方形ABCD的边AB、BC为直径画半圆，若正方形的边长为a，则阴影部分面积 ，利用 数学原理求得．
【答案】分析：易知两段半圆的交点即为正方形的对称中心（设为O），连接AC、BD；将两个弓形分别进行旋转，即可将所求的阴影部分的面积转化为半个正方形的面积，由此得解．
解答：
解：易知：两半圆的交点即为正方形的中心，设此点为O，连接AC，则AC必过点O，连接OB；
将弓形OmB绕点O旋转并与弓形OaA重合；
同理将弓形OnB绕点O旋转并与弓形ObC重合，
此时阴影部分的面积正好是△ADC的面积，即正方形面积的一半；
故阴影部分的面积为：
a2，利用的是旋转变换数学原理．
点评：此题主要考查了正方形的性质以及旋转的性质，难度适中．
解答：
解：易知：两半圆的交点即为正方形的中心，设此点为O，连接AC，则AC必过点O，连接OB；将弓形OmB绕点O旋转并与弓形OaA重合；
同理将弓形OnB绕点O旋转并与弓形ObC重合，
此时阴影部分的面积正好是△ADC的面积，即正方形面积的一半；
故阴影部分的面积为：
a2，利用的是旋转变换数学原理．点评：此题主要考查了正方形的性质以及旋转的性质，难度适中．
练习册系列答案
相关题目
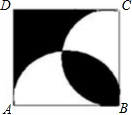如图，分别以正方形ABCD的边AB、BC为直径画半圆，若正方形的边长为a，则阴影部分面积
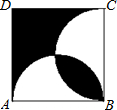如图，分别以正方形ABCD的边AB、BC为直径画半圆，若正方形的边长为a，则阴影部分面积
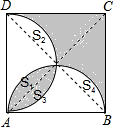小华在某课外书上看到了这样一道题：“如图，分别以正方形ABCD的边AB、AD为直径画半圆．若正方形的边长为a，求阴影部分的面积．”从表面上看，图中的阴影部分是复杂且比较分散的图形，要直接计算它的面积还是有困难的，但小华仔细考虑过后，只是将正方形的对角线AC、BD连接起来，然后利用自己所学的“图形的旋转”知识很简便地就将本题解决了，你知道他是怎样做的吗？