题目内容
【题目】如图,在边长为3的正方形![]() 中,点
中,点![]() 是
是![]() 边上的点,
边上的点,![]() ,
,![]() ;且
;且![]() 交正方形外角的平分线
交正方形外角的平分线![]() 于点
于点![]() ,交边
,交边![]() 于点
于点![]() .
.
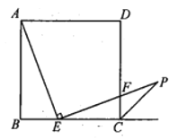
(1)求证:AE=EP;
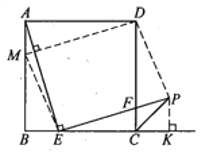
(2)在![]() 边上是否存在点
边上是否存在点![]() ,使得四边形
,使得四边形![]() 是平行四边形?若存在,请给予证明;若不存在,请说明理由.
是平行四边形?若存在,请给予证明;若不存在,请说明理由.
【答案】(1)详见解析;(2)存在,见解析.
【解析】
(1)在AB上取BN=BE,根据已知及正方形的性质利用ASA判定△ANE≌△ECP,从而得到AE=EP;
(2)先证△DAM≌△ABE,再证![]() ,进而可得四边形DMEP是平行四边形.
,进而可得四边形DMEP是平行四边形.
(1)
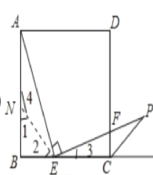
证明:在AB上截取
BN=BE,如图所示
∵四边形ABCD为正方形,
∴AB=BC.∠B=90°
∴AN=EC,∠1=∠2=45°
∴∠4=135°
∵CP为正方形ABCD的外角平分线,
∴∠PCB=135°
∴∠PCB=∠4.
∵∠AEP=90°
∴∠BEA+∠3=90°
∵∠BAE+∠BEA=90°
∴∠3=∠BAE
∴△ANE≌△ECP
∴AE=EP;
(2)存在.
如图,作![]() 且与
且与![]() 交于点
交于点![]() ,则有
,则有![]() .连结
.连结![]() 、
、![]() ,过
,过![]() 作
作![]() 于
于![]() .可证得
.可证得![]() ,从而
,从而![]() ,所以
,所以![]() ,
,
依题意可设![]() ,由(1)知
,由(1)知![]() ,得
,得![]() ,则
,则![]() ,所以
,所以![]() ,解得
,解得![]() ,则
,则![]() ,于是
,于是![]() ,所以
,所以![]() ,则得
,则得![]() ,所以四边形
,所以四边形![]() 为平行四边形.
为平行四边形.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目