题目内容
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E在AC上(点E与A、C都不重合),点F在斜边AB上(点F与A、B都不重合).
(Ⅰ)若EF平分Rt△ABC的周长,设AE=x,△AEF的面积为y,写出y与x之间的函数关系式,并指出x的取值范围;
(Ⅱ)试问:是否存在直线EF将Rt△ABC的周长和面积同时平分?若存在,求出AE的长;若不存在,说明理由.

(Ⅰ)若EF平分Rt△ABC的周长,设AE=x,△AEF的面积为y,写出y与x之间的函数关系式,并指出x的取值范围;
(Ⅱ)试问:是否存在直线EF将Rt△ABC的周长和面积同时平分?若存在,求出AE的长;若不存在,说明理由.

(Ⅰ)在直角三角形ABC中,AC=3,BC=4,所以AB=5
∴三角形ABC的周长为12,又因EF平分三角形ABC的周长,
∴AE+AF=6,而AE=x,
∴AF=6-x
过点F作FD⊥AC于D
则
=sinA=
=
∴
=
∴DF=
(6-x)
所以y=
AE•DF=
x•
(6-x)=-
x2+
x(1<x<3)
(Ⅱ)这样的EF存在,
S△ABC=
BC•AC=
×4×3=6
∵EF平分△ABC的面积,
所以-
x2+
x=3
解得:x=
∵1<x<3
∴x取
∴6-x=6-
=
<5
符合题意,所以这样的EF存在,此时AE=
.
∴三角形ABC的周长为12,又因EF平分三角形ABC的周长,
∴AE+AF=6,而AE=x,
∴AF=6-x
过点F作FD⊥AC于D
则
| DF |
| AF |
| BC |
| AB |
| 4 |
| 5 |
∴
| DF |
| 6-x |
| 4 |
| 5 |
∴DF=
| 4 |
| 5 |
所以y=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| 5 |
| 12 |
| 5 |
(Ⅱ)这样的EF存在,
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∵EF平分△ABC的面积,
所以-
| 2 |
| 5 |
| 12 |
| 5 |
解得:x=
6±
| ||
| 2 |
∵1<x<3
∴x取
6-
| ||
| 2 |
∴6-x=6-
6-
| ||
| 2 |
6+
| ||
| 2 |
符合题意,所以这样的EF存在,此时AE=
6-
| ||
| 2 |

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
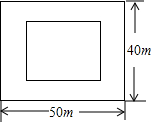

 米150元,设绿化区的长边长为x米.
米150元,设绿化区的长边长为x米.