题目内容
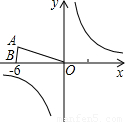
已知:等腰△OAB在直角坐标系中的位置如图,点A坐标为(-3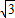 ,3),点B坐标为(-6,0).
,3),点B坐标为(-6,0).(1)若将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数y=
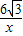 的图象上,求a的值;
的图象上,求a的值;(2)若△OAB绕点O按逆时针方向旋转α度(0<α<360).
①当α=30°时,点B恰好落在反比例函数y=
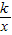 的图象上,求k的值;
的图象上,求k的值;②问点A、B能否同时落在①中的反比例函数的图象上?若能,直接写出α的值;若不能,请说明理由.
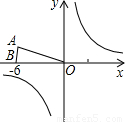
【答案】分析:(1)根据点A坐标为(-3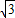 ,3),将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数y=
,3),将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数y=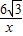 的图象上,则平移以后点的纵坐标是3,把y=3代入解析式就可以得到A点平移后的点的横坐标,得到a的值;
的图象上,则平移以后点的纵坐标是3,把y=3代入解析式就可以得到A点平移后的点的横坐标,得到a的值;
(2)△OAB绕点O按逆时针方向旋转30度,就可以求出旋转后点的坐标,代入反比例函数y=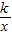 的解析式,就可以求出k的值.
的解析式,就可以求出k的值.
解答:解:(1)设点A平移后落在双曲线y=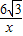 上时,坐标为A′(m,n),
上时,坐标为A′(m,n),
∵A(-3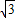 ,3),由已知得n=3,(1分)
,3),由已知得n=3,(1分)
代入y=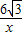 ,求得m=2
,求得m=2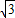 ;(2分)
;(2分)
∴平移的距离a=|2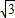 -(-3
-(-3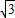 )|=5
)|=5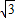 ;
;
(2)①B′的纵坐标是:-6sinα=-6×sin30°=-3,
横坐标是:-6cosα=-6cos30°=-3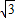 ,
,
B′的坐标是:(-3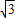 ,-3)(5分)
,-3)(5分)
∴k=-3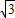 ×(-3)=9
×(-3)=9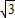 ;(6分)
;(6分)
②∵点A坐标为(-3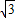 ,3),
,3),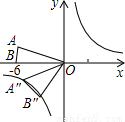
∴OA=6,
∴OA=OB=6,
∴tan∠AOB=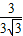 =
=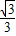 ,
,
∴∠AOB=30°,
当∠BOA″=30°时,则∠BOB″=60°,
A″的坐标为(-3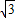 ,-3),B″的坐标为(-3,-3
,-3),B″的坐标为(-3,-3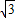 ),
),
∴此时点A、B能同时落在①中的反比例函数的图象上;
同理:α=240°也符合题意;
∴α=60°或240°.
点评:本题主要考查了直角三角形的解法,利用待定系数法求函数的解析式.同学们要熟练掌握平移及旋转的知识点.
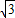 ,3),将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数y=
,3),将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数y=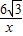 的图象上,则平移以后点的纵坐标是3,把y=3代入解析式就可以得到A点平移后的点的横坐标,得到a的值;
的图象上,则平移以后点的纵坐标是3,把y=3代入解析式就可以得到A点平移后的点的横坐标,得到a的值;(2)△OAB绕点O按逆时针方向旋转30度,就可以求出旋转后点的坐标,代入反比例函数y=
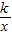 的解析式,就可以求出k的值.
的解析式,就可以求出k的值.解答:解:(1)设点A平移后落在双曲线y=
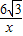 上时,坐标为A′(m,n),
上时,坐标为A′(m,n),∵A(-3
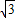 ,3),由已知得n=3,(1分)
,3),由已知得n=3,(1分)代入y=
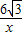 ,求得m=2
,求得m=2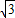 ;(2分)
;(2分)∴平移的距离a=|2
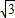 -(-3
-(-3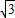 )|=5
)|=5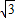 ;
;(2)①B′的纵坐标是:-6sinα=-6×sin30°=-3,
横坐标是:-6cosα=-6cos30°=-3
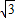 ,
,B′的坐标是:(-3
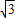 ,-3)(5分)
,-3)(5分)∴k=-3
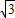 ×(-3)=9
×(-3)=9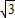 ;(6分)
;(6分)②∵点A坐标为(-3
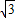 ,3),
,3),
∴OA=6,
∴OA=OB=6,
∴tan∠AOB=
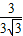 =
=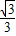 ,
,∴∠AOB=30°,
当∠BOA″=30°时,则∠BOB″=60°,
A″的坐标为(-3
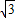 ,-3),B″的坐标为(-3,-3
,-3),B″的坐标为(-3,-3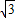 ),
),∴此时点A、B能同时落在①中的反比例函数的图象上;
同理:α=240°也符合题意;
∴α=60°或240°.
点评:本题主要考查了直角三角形的解法,利用待定系数法求函数的解析式.同学们要熟练掌握平移及旋转的知识点.

练习册系列答案
相关题目
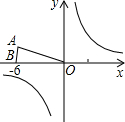 已知:等腰△OAB在直角坐标系中的位置如图,点A坐标为(-3
已知:等腰△OAB在直角坐标系中的位置如图,点A坐标为(-3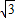 ,3),点B坐标为(-6,0).
,3),点B坐标为(-6,0).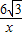 的图象上,求a的值;
的图象上,求a的值;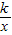 的图象上,求k的值;
的图象上,求k的值;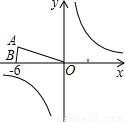
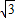 ,3),点B坐标为(-6,0).
,3),点B坐标为(-6,0).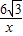 的图象上,求a的值;
的图象上,求a的值;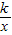 的图象上,求k的值;
的图象上,求k的值;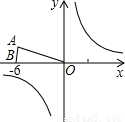
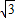 ,3),点B坐标为(-6,0).
,3),点B坐标为(-6,0).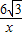 的图象上,求a的值;
的图象上,求a的值;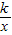 的图象上,求k的值;
的图象上,求k的值;