题目内容
 如图,半径为2
如图,半径为2| 5 |
| 15 |
| 15 |
分析:先求出OM,ON,进而证得四边形OMPN是矩形,所以OP=PM,利用勾股定理可以求出OP的长.
解答:解:作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,
由垂径定理得:OM2=(2
)2-42=4,ON2=(2
)2-32=11,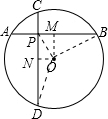
∵弦AB、CD互相垂直,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∴OP=
=
=
.
故答案为:
.
由垂径定理得:OM2=(2
| 5 |
| 5 |

∵弦AB、CD互相垂直,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∴OP=
| OM2+ON2 |
| 4+11 |
| 15 |
故答案为:
| 15 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
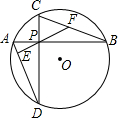 如图,半径为2
如图,半径为2 如图,半径为2
如图,半径为2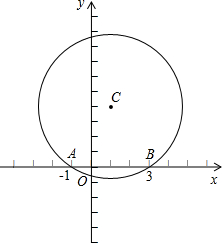 3,0)两点,且点C在x轴的上方.
3,0)两点,且点C在x轴的上方. 如图,半径为
如图,半径为