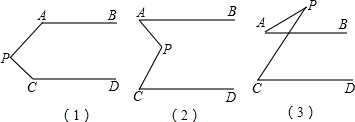Question

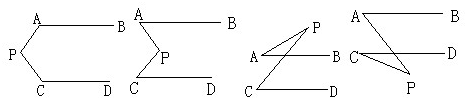
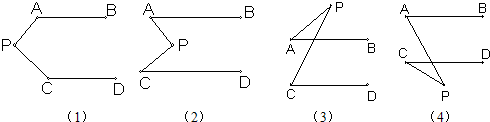
26、已知AB∥CD，分别探讨下列四个图形中∠APC和∠PAB、∠PCD的关系．（只要求直接写出），并请你从所得四个关系中任意选出一个说明理由．

（1）

∠APC+∠PAB+∠PCD=360°

        （2）

∠APC=∠PAB+∠PCD

        （3）

∠APC=∠PCD-∠PAB

         （4）

∠APC=∠PAB-∠PCD

．

Answer 1

分析：①②过P作EF∥AB，根据平行公理的推论得到AB∥CD∥EF，根据平行线的性质即可得到答案；③根据平行线的性质得到∠PEB=∠PCD，根据三角形的外角性质即可得到答案；④设PA交CD于E，由AB∥CD，得到∠PAB=∠AED，根据∠AED=∠PCD+∠APC，即可得到答案．

解答：解：①故答案为：∠APC+∠PAB+∠PCD=360°．

②故答案为：∠APC=∠PAB+∠PCD．

③故答案为：∠APC=∠PCD-∠PAB．

④解：∠APC=∠PAB-∠PCD，
理由是：
设PA交CD于E，
∵AB∥CD，
∴∠PAB=∠AED，
∵∠AED=∠PCD+∠APC，
∴∠APC=∠PAB-∠PCD，
故答案为：∠APC=∠PAB-∠PCD．

点评：本题主要考查对平行线的性质，平行公理及推论，三角形的外角性质等知识点的理解和掌握，能灵活运用性质进行推理是解此题的关键．