题目内容
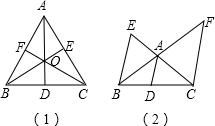利用塞瓦定理可以简便地证明重心定理、内心定理和垂心定理：
分析：①由AD，BE，CF是△ABC的中线，根据中线的性质得到
•
•
=1，得到AD，BE，CF三条中线交于一点．
②由AD，BE，CF是△ABC的内角平分线，根据角平分线定理得到
=
，
=
，
=
．把它们分别相乘然后利用塞瓦定理，得到AD，BE，CF三条内角平分线交于一点．
③由AD，BE，CF是△ABC的三条高线，则△ABD∽△CBF，得到
=
；△ACD∽△BCE，得到
=
；△ABE∽△ACF，得到
=
．把它们分别相乘然后利用塞瓦定理，得到AD，BE，CF三条高线或延长线交于一点．
| BD |
| DC |
| CE |
| CA |
| AF |
| FB |
②由AD，BE，CF是△ABC的内角平分线，根据角平分线定理得到
| BD |
| DC |
| AB |
| AC |
| CE |
| EA |
| BC |
| AB |
| AF |
| FB |
| AC |
| BC |
③由AD，BE，CF是△ABC的三条高线，则△ABD∽△CBF，得到
| BD |
| FB |
| AB |
| BC |
| CE |
| CD |
| BC |
| AC |
| AF |
| AE |
| AC |
| AB |
解答：证明：①如果AD，BE，CF是△ABC的中线，则BD=DC，CE=AE，AF=FB．
∴
•
•
=1，
∴AD，BE，CF三条中线交于一点；
②如果AD，BE，CF是△ABC的内角平分线，
则
=
，
=
，
=
．
∴
•
•
=
•
•
=1，
因此AD，BE，CF三条内角平分线交于一点；
③如果AD，BE，CF是△ABC的三条高线，
∵△ABD∽△CBF，
∴
=
，
∵△ACD∽△BCE，
∴
=
，
∵△ABE∽△ACF，
∴
=
．
∴
•
•
=
•
•
=
．
•
=1，
因此AD，BE，CF三条高线或延长线交于一点．
∴
| BD |
| DC |
| CE |
| CA |
| AF |
| FB |
∴AD，BE，CF三条中线交于一点；
②如果AD，BE，CF是△ABC的内角平分线，
则
| BD |
| DC |
| AB |
| AC |
| CE |
| EA |
| BC |
| AB |
| AF |
| FB |
| AC |
| BC |
∴
| BD |
| DC |
| CE |
| EA |
| AF |
| FB |
| AB |
| AC |
| BC |
| AB |
| AC |
| BC |
因此AD，BE，CF三条内角平分线交于一点；
③如果AD，BE，CF是△ABC的三条高线，
∵△ABD∽△CBF，
∴
| BD |
| FB |
| AB |
| BC |
∵△ACD∽△BCE，
∴
| CE |
| CD |
| BC |
| AC |
∵△ABE∽△ACF，
∴
| AF |
| AE |
| AC |
| AB |
∴
| BD |
| DC |
| CE |
| EA |
| AF |
| FB |
| BD |
| FB |
| CE |
| DC |
| AF |
| EA |
| AB |
| BC |
| BC |
| AC |
| AC |
| AB |
因此AD，BE，CF三条高线或延长线交于一点．
点评：本题考查了塞瓦定理的运用．也考查了三角形中线、角平分线和高的性质以及三角形相似的性质．
练习册系列答案
相关题目