题目内容
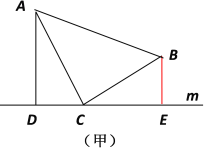
【题目】如图:△ABC中CA=CB, ∠ACB=90°,直线m经过点C,AD⊥m,BE⊥m,垂足分别是点D、E.
(1)在图(甲)中,求证:△ACD≌△CBE.你能探索出线段AD、BE、DE之间的关系吗?
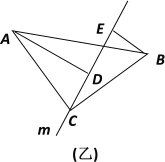
(2)在图(乙)中上面的结论还成立吗?为什么?
【答案】(1)证明见解析,DE=AD+BE;(2)成立,理由见解析
【解析】试题分析:(1)根据垂直的性质,可根据“AAS”证明△ADC ≌△CEB,然后根据全等三角形的性质证明即可;
(2)同(1)的证明方法直接可证明.
试题解析:DE=AD+BE
(1)证明:∵AD⊥m ∴∠DAC﹢∠ACD=∠ADC=90°
∵∠ACB=90°∴∠ACD+∠BCE=90°
∴∠DAC=∠BCE
∵BE⊥m ∴∠BEC=90°
在△ADC 和△CEB中
∠ADC=∠CEB=90°
∠DAC=∠BCE
CA=CB
∴△ADC ≌△CEB (AAS)
∴AD=CE DC=BE (全等三角形的对应边相等)
∵DE=DC+CE ∴DE=AD+BE
(2) 在(乙)图中上面的结论仍然成立.
证明:∵AD⊥m ∴∠ADC=90°∠ACD+∠CAD=90°
∵BE⊥m ∴∠CEB=90°
∵∠ACB=90°∴∠ACD+∠BCE=90°
∴∠DAC=∠ECB
在△ADC 和△CEB中
∠ADC=∠CEB=90°
∠DAC=∠ECB
CA=CB
∴△ADC ≌△CEB (AAS)
∴AD=CE DC=BE (全等三角形的对应边相等)
∵DE=DC+CE ∴DE=AD+BE

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目