Question

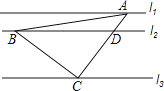
【题目】如图是由边长相同的小正方形组成的网格，A，B，P，Q四点均在正方形网格的格点上，线段AB，PQ相交于点M，则图中∠QMB的正切值是（ ）

A.
B.1
C.
D.2

Answer 1

【答案】A
【解析】解：连接AP，QB，

由网格可得：∠PAB=∠QBA=90°，
又∵∠AMP=∠BMQ，
∴△PAM∽△QBM，
∴ = ，
∵AP=3 ，BQ= ，AB=2 ，
∴ = ，解得：AM= ，
∴tan∠QMB=tan∠PMA= = = ．
故选：A．
根据题意得出△PAM∽△QBM，进而结合勾股定理得出AP=3 ，BQ= ，AB=2 ，进而求出答案．此题主要考查了勾股定理以及相似三角形的判定与性质以及锐角三角函数关系，正确得出△PAM∽△QBM是解题关键．