题目内容
比较左、右两图的阴影部分面积，可以得到因式分解公式( ).
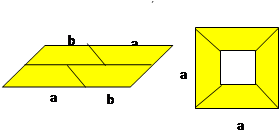
A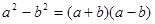． | B． |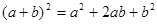
C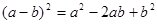． | D． |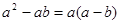
A
过A作AE⊥BC于E，过D作DF⊥BC于F，得出矩形AEFD，求出BE值，求出高AE，根据矩形和正方形的面积公式求出第一个和第二个图形阴影部分的面积，根据阴影部分的面积相等即可得出答案．
解：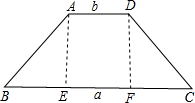
过A作AE⊥BC于E，过D作DF⊥BC于F，
∵AD∥BC，
∴∠AEF=∠DAE=∠DFE=90°，
则四边形ADFE是矩形，
∴AD=EF，BE=CF=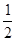
（a-b），
由图形可知：∠B=45°，
∴AE=BE=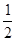（a-b），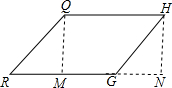
∴第一个图形阴影部分的面积等于矩形QMNH的面积，是（a+b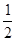）×（a-b）×2=（a+b）（a-b），
第二个图形阴影部分的面积是a2-b2，
∴a2-b2=（a+b）（a-b），
故选A．
本题考查了对平方差公式的几何图形的运用，表示出阴影部分的面积是解此题的关键．
解：
过A作AE⊥BC于E，过D作DF⊥BC于F，
∵AD∥BC，
∴∠AEF=∠DAE=∠DFE=90°，
则四边形ADFE是矩形，
∴AD=EF，BE=CF=
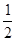（a-b），由图形可知：∠B=45°，
∴AE=BE=
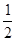（a-b），∴第一个图形阴影部分的面积等于矩形QMNH的面积，是（a+b）×
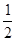（a-b）×2=（a+b）（a-b），第二个图形阴影部分的面积是a2-b2，
∴a2-b2=（a+b）（a-b），
故选A．
本题考查了对平方差公式的几何图形的运用，表示出阴影部分的面积是解此题的关键．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
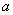的倒数大3的数：________________；
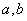的平方差为：__________________；
