题目内容
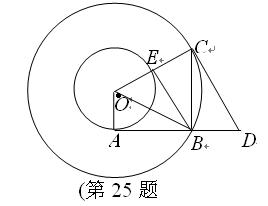
如图所示,在以O为圆心的两个同心圆中,小圆的半径为1,AB与小圆相切于点A,与大圆相交于点B,大圆的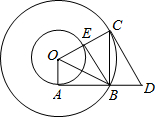 弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.
弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.(1)求证:△AOB∽△BDC;
(2)设大圆的半径为x,CD的长为y:
①求y与x之间的函数关系式;
②当BE与小圆相切时,求x的值.
分析:(1)由AB与小圆相切,CD与大圆相切,根据切线性质可得∠OAB与∠OCD相等,都为直角,又BC与AB垂直,根据垂直定义得到∠CBA与∠CBD都为直角,则∠1+∠OBC与∠2+∠OCB和都为90°,由OC=OB,根据“等边对等角”得到∠OBC=∠OCB,根据等角的余角相等,得到∠1=∠2,由两对对应角相等的两三角形相似得证;
(2)①过O作OF垂直于BC,由三个角都为直角的四边形为矩形得到ABOF为矩形,根据矩形的对边相等,得到FB=OA,由OA的长得到FB的长,又BC为大圆的弦,利用垂径定理得到BC=2BF,从而求出BC的长,在直角三角形OAB中,由OA=1,OB=x,利用勾股定理表示出AB,由(1)得到的三角形相似得比例,把相应的值代入即可得到y与x的关系式;
②当BE与小圆相切时,根据切线性质得到OE与BE垂直,由OE和OC表示出EC的长,根据切线长定理得到BE=BA,表示出EB,在直角三角形ECB中,由EC,EB及BC的长,利用勾股定理列出关于x的方程,求出方程的解即可得到x的值.
(2)①过O作OF垂直于BC,由三个角都为直角的四边形为矩形得到ABOF为矩形,根据矩形的对边相等,得到FB=OA,由OA的长得到FB的长,又BC为大圆的弦,利用垂径定理得到BC=2BF,从而求出BC的长,在直角三角形OAB中,由OA=1,OB=x,利用勾股定理表示出AB,由(1)得到的三角形相似得比例,把相应的值代入即可得到y与x的关系式;
②当BE与小圆相切时,根据切线性质得到OE与BE垂直,由OE和OC表示出EC的长,根据切线长定理得到BE=BA,表示出EB,在直角三角形ECB中,由EC,EB及BC的长,利用勾股定理列出关于x的方程,求出方程的解即可得到x的值.
解答: (1)证明:
(1)证明:
∵AB与小圆相切于点A,CD与大圆相切于点C,
∴∠OAB=∠OCD=90°,
∵BC⊥AB,
∴∠CBA=∠CBD=90°,(1分)
∵∠1+∠OBC=90°,∠2+∠OCB=90°,
又∵OC=OB,
∴∠OBC=∠OCB,
∴∠1=∠2,(2分)
∴△AOB∽△BDC;(3分)
(2)解:①过点O作OF⊥BC于点F,则四边形OABF是矩形(4分)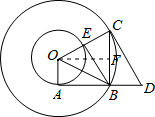
∴BF=OA=1,
由垂径定理,得BC=2BF=2,(5分)
在Rt△AOB中,OA=1,OB=x
∴AB=
=
,(6分)
由(1)得△AOB∽△BDC
∴
=
,即
=
,
∴y=
=
;(7分)
②当BE与小圆相切时,OE⊥BE,
∵OE=1,OC=x,
∴EC=x-1,BE=AB=
,(8分)
在Rt△BCE中,根据勾股定理得:EC2+BE2=BC2,
即(x-1)2+(
)2=22,(9分)
解得:x1=2,x2=-1(舍去),(10分)
∴当BE与小圆相切时,x=2.(11分)
 (1)证明:
(1)证明:∵AB与小圆相切于点A,CD与大圆相切于点C,
∴∠OAB=∠OCD=90°,
∵BC⊥AB,
∴∠CBA=∠CBD=90°,(1分)
∵∠1+∠OBC=90°,∠2+∠OCB=90°,
又∵OC=OB,
∴∠OBC=∠OCB,
∴∠1=∠2,(2分)
∴△AOB∽△BDC;(3分)
(2)解:①过点O作OF⊥BC于点F,则四边形OABF是矩形(4分)

∴BF=OA=1,
由垂径定理,得BC=2BF=2,(5分)
在Rt△AOB中,OA=1,OB=x
∴AB=
| OB2-OA2 |
| x2-1 |
由(1)得△AOB∽△BDC
∴
| OB |
| CD |
| AB |
| BC |
| x |
| y |
| ||
| 2 |
∴y=
| 2x | ||
|
2x
| ||
| x2-1 |
②当BE与小圆相切时,OE⊥BE,
∵OE=1,OC=x,
∴EC=x-1,BE=AB=
| x2-1 |
在Rt△BCE中,根据勾股定理得:EC2+BE2=BC2,
即(x-1)2+(
| x2-1 |
解得:x1=2,x2=-1(舍去),(10分)
∴当BE与小圆相切时,x=2.(11分)
点评:此题考查了切线的性质,相似三角形的判定与性质,勾股定理及垂径定理.遇到切线,连接圆心与切点,是常常连接的辅助线,借助图形,由切线的性质构造直角三角形,然后利用勾股定理解决问题.熟练掌握切线的性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 53、如图所示,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E,求证:CD与小圆相切.
53、如图所示,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E,求证:CD与小圆相切.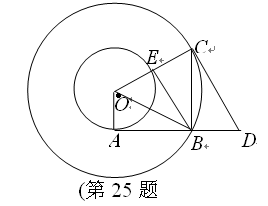
 A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.
A,与大圆相交于点B,大圆的弦BC⊥AB于点B,过点C作大圆的切线CD交AB的延长线于点D,连接OC交小圆于点E,连接BE、BO.