题目内容
用列表法画二次函数y=x2+bx+c的图象时先列一个表,当表中对自变量x的值以相等间隔的值增加时,函数y所对应的值依次为:20,56,110,182,274,380,506,650,其中有一个值不正确,这个不正确的值是( )A.506
B.380
C.274
D.182
【答案】分析:因为x的值以相等间隔的值增加,所以只要设出相邻的两个自变量的值为x1、x2代入求出差值,再由具体的计算看是否成规律变化找出即可.
解答:解:设相邻的两个自变量的值为x1、x2,代入y=x2+bx+c,
计算差值为:y1-y2=(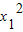 -
-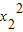 )+b(x1-x2)=(x1-x2)(x1+x2+b),因此函数值之间的差值间隔是相等的,
)+b(x1-x2)=(x1-x2)(x1+x2+b),因此函数值之间的差值间隔是相等的,
即含有公因数x1-x2,
计算各个差值为
56-20=36;110-56=54;182-110=72;274-182=92;380-274=106;506-380=126;650-506=144,
36、54、72都含有公因数9,即x1-x2=9,
而92不含有因数9,
∴可以断定是274错误了.
故选C.
点评:此题主要考查画二次函数图象时,一般利用函数对称性取值描点,使点之间的数据间隔相等.
解答:解:设相邻的两个自变量的值为x1、x2,代入y=x2+bx+c,
计算差值为:y1-y2=(
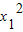 -
-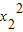 )+b(x1-x2)=(x1-x2)(x1+x2+b),因此函数值之间的差值间隔是相等的,
)+b(x1-x2)=(x1-x2)(x1+x2+b),因此函数值之间的差值间隔是相等的,即含有公因数x1-x2,
计算各个差值为
56-20=36;110-56=54;182-110=72;274-182=92;380-274=106;506-380=126;650-506=144,
36、54、72都含有公因数9,即x1-x2=9,
而92不含有因数9,
∴可以断定是274错误了.
故选C.
点评:此题主要考查画二次函数图象时,一般利用函数对称性取值描点,使点之间的数据间隔相等.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目