题目内容
【题目】下列说法:
①若三角形一边上的中线和这边上的高重合,则这个三角形是等腰三角形;
②若等腰三角形一腰上的高与底边的夹角为20°,则顶角为40°;
③如果直角三角形的两边长分别为3、4,那么斜边长为5;
④斜边上的高和一直角边分别相等的两个直角三角形全等.
其中正确的说法有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】如图,
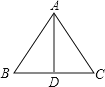
∵AD是高,∴AD⊥BC,∵BD=CD,∴AB=AC,即△ABC是等腰三角形,∴①正确;
如图,
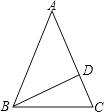
∵BD⊥AC,∴∠BDC=90,∵∠DBC=20,∴∠C=70,∵AB=AC,∴∠ABC=∠C=70,∴∠A=1807070=40,∴②正确;
可能斜边是4,一条直角边是3,∴③错误;
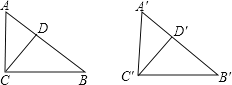
如图,在Rt△ADC和Rt△A′D′C′中,AC=A′C′,CD=C′D′,符合HL定理,即能推出Rt△ADC≌Rt△A′D′C′,∴∠A=∠A′,再根据ASA即可推出Rt△ACB≌Rt△A′C′B′,∴④正确;即正确的有3个,故选C.

【题目】“中国汉字听写大会”是由中央电视台和国家语言文字工作委员会联合主办的节目,希望通过节目的播出,能吸引更多的人关注对汉字文化的学习.某校也开展了一次“汉字听写”比赛,每位参赛学生听写40个汉字.比赛结束后随机抽取部分学生的听写结果,按听写正确的汉字个数x绘制成了以下不完整的统计图.

根据以上信息回答下列问题:
(1)本次共随机抽取了_______名学生进行调查,听写正确的汉字个数x在_____________范围内的人数最多;
(2)补全频数分布直方图;
(3)各组的组中值如下表所示.若用各组的组中值代表各组每位学生听写正确的汉字个数,求被调查学生听写正确的汉字个数的平均数;
听写正确的汉字个数x | 组中值 |
1≤x<11 | 6 |
11≤x<21 | 16 |
21≤x<31 | 26 |
31≤x<41 | 36 |
(4)该校共有1350名学生,如果听写正确的汉字个数不少于21个定为良好,请你估计该校本次“汉字听写”比赛达到良好的学生人数.




