题目内容
【题目】如图,根据图中信息解答下列问题:
(1)关于x的不等式ax+b>0的解集是________;
(2)关于x的不等式mx+n<1的解集是________;
(3)当x为何值时,y1≤y2?
(4)当x<0时,比较y2与y1的大小关系.
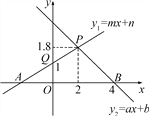
【答案】(1)x<4;(2)x<0;(3) x≤2;(4)y2>y1.
【解析】试题分析:(1)利用直线y2=ax+b与x轴的交点为(4,0),然后利用函数图象可得到不等式ax+b>0的解集.
(2)利用直线y=mx+n与x轴的交点为(0,1),然后利用函数图象可得到不等式mx+n<1的解集.
(3)结合两条直线的交点坐标为(2,1.8)来求得y1≤y2解集.
(4)结合函数图象直接写出答案.
试题解析:(1)∵直线y2=ax+b与x轴的交点是(4,0),
∴当x<4时,y2>0,即不等式ax+b>0的解集是x<4;
故答案是:x<4;
(2)∵直线y1=mx+n与y轴的交点是(0,1),
∴当x<0时,y1<1,即不等式mx+n<1的解集是x<0;.
故答案是:x<0;
(3)由一次函数的图象知,两条直线的交点坐标是(2,18),当函数y1的图象在y2的下面时,有x≤2,
所以当x≤2时,y1≤y2;
(4)如图所示,当x<0时,y2>y1.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目





