Question

【题目】已知二次函数y=x2+px+q图象的顶点M为直线y=x+与y=-x+m-1的交点，

（1）用含m的代数式来表示顶点M的坐标（直接写出答案）；

（2）当x≥2时，二次函数y=x2+px+q与y=x+的值均随x的增大而增大，求m的取值范围

（3）若m＝6，当x取值为t-1≤x≤t+3时，二次函数y最小值=2，求t的取值范围

Answer 1

【答案】（1）M坐标为(，)；（2）m的取值范围为m≤；（3）0≤t≤4．

【解析】

试题分析：（1）已知直线y=x+和y=-x+m-1，列出方程求出x，y的等量关系式即可求出点M的坐标；

（2）根据题意得出≤2，解不等式求出m的取值；

（3）当t-1≤3时，当3≤t+3时，二次函数y最小值=2，解不等式组即可求得．

试题解析：（1）由，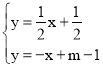

解得 ，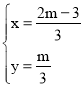

即交点M坐标为(，)；

（2）∵二次函y=x2+px+q图象的顶点M为直线y=x+与y=-x+m-1的交点为(，)，且当x≥2时，二次函数y=x2+px+q与y=x+的值均随x的增大而增大，

∴≤2，

解得m≤，

∴m的取值范围为m≤；

（3）∵m=6，

∴顶点为（3，2），

∴抛物线为y=（x-3）2+2，

∴函数y有最小值为2，

∵当x取值为t-1≤x≤t+3时，二次函数y最小值=2，

∴t-1≤3，t+3≥3，

解得0≤t≤4．