题目内容
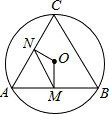 如图,在等边△ABC中,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=1,那么△ABC的面积为
如图,在等边△ABC中,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=1,那么△ABC的面积为
- A.3
- B.

- C.4
- D.

B
分析:先根据OM⊥AB,ON⊥AC,垂足分别为M、N,可知MN是△ABC的中位线,再根据MN=1可求出BC的长,再由等边三角形的性质即可求出△ABC的面积.
解答:∵⊙O是等边△ABC的外接圆,OM⊥AB,ON⊥AC,垂足分别为M、N,
∴M、N分别是AC、AB的中点,
∴MN是等边△ABC的中位线,
∵MN=1,
∴AB=AC=BC=2MN=2,
∴S△ABC= ×2×2×sin60°=2×
×2×2×sin60°=2× =
= .
.
故选B.
点评:本题考查的是垂径定理、等边三角形的性质及三角形中位线定理,根据题意判断出MN是等边△ABC的中位线是解答此题的关键.
分析:先根据OM⊥AB,ON⊥AC,垂足分别为M、N,可知MN是△ABC的中位线,再根据MN=1可求出BC的长,再由等边三角形的性质即可求出△ABC的面积.
解答:∵⊙O是等边△ABC的外接圆,OM⊥AB,ON⊥AC,垂足分别为M、N,
∴M、N分别是AC、AB的中点,
∴MN是等边△ABC的中位线,
∵MN=1,
∴AB=AC=BC=2MN=2,
∴S△ABC=
 ×2×2×sin60°=2×
×2×2×sin60°=2× =
= .
.故选B.
点评:本题考查的是垂径定理、等边三角形的性质及三角形中位线定理,根据题意判断出MN是等边△ABC的中位线是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
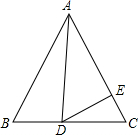 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
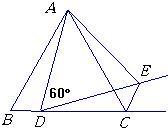 16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是
16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是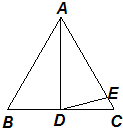 21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°.
21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°.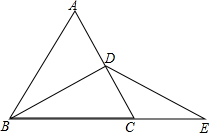 如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm.
如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm. 如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证:
如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证: