题目内容
(2007•大连)为了鼓励小强勤做家务,培养他的劳动意识,小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x小时,该月可得(即下月他可获得)的总费为y元,则y(元)和x(小时)之间的函数图象如图所示.(1)根据图象,请你写出小强每月的基本生活费为多少元;父母是如何奖励小强家务劳动的?
(2)写出当0≤x≤20时,相对应的y与x之间的函数关系式;
(3)若小强5月份希望有250元费用,则小强4月份需做家务多少时间?
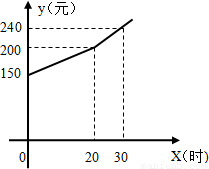
【答案】分析:(1)由图象可看出,x=0时,即小强不做家务劳动时所得费用为基本生活费150元;如果小强每月家务劳动时间不超过20小时,则每小时奖励(200-150)÷20=2.5元;超过20小时,超过部分每小时奖励(240-200)÷10=4元;
(2)当0≤x≤20时,y与x之间的成一次函数,且经过点(0,150)和点(20,200),使用待定系数法求解即可;
(3)由图象可求出,当x≥20时,y与x的函数关系式,把y=250代入即可.
解答:解:(1)依题意得小强父母给小强的每月基本生活费为150元;
如果小强每月家务劳动时间不超过20小时,每小时获奖励2.5元;
如果小强每月家务劳动时间超过20小时,那么20小时按每小时2.5元奖励,超过部分按每小时4元奖励.
(2)∵当0≤x≤20时,图象经过(0,150)(20,200),
∴y=2.5x+150;
(3)当x≥20时,图象经过点(20,200)和点(30,240),
∴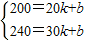 ,
,
解得: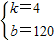 ,
,
∴y与x的函数关系式是:y=4x+120.
由题意得,4x+120=250,
解得x=32.5.
答:当小强4月份家务劳动32.5小时,5月份可得到的费用为250元.
点评:本题考查识图能力,也考查了利用待定系数法求一次函数关系式,正确理解题意比较关键.
(2)当0≤x≤20时,y与x之间的成一次函数,且经过点(0,150)和点(20,200),使用待定系数法求解即可;
(3)由图象可求出,当x≥20时,y与x的函数关系式,把y=250代入即可.
解答:解:(1)依题意得小强父母给小强的每月基本生活费为150元;
如果小强每月家务劳动时间不超过20小时,每小时获奖励2.5元;
如果小强每月家务劳动时间超过20小时,那么20小时按每小时2.5元奖励,超过部分按每小时4元奖励.
(2)∵当0≤x≤20时,图象经过(0,150)(20,200),
∴y=2.5x+150;
(3)当x≥20时,图象经过点(20,200)和点(30,240),
∴
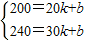 ,
,解得:
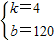 ,
,∴y与x的函数关系式是:y=4x+120.
由题意得,4x+120=250,
解得x=32.5.
答:当小强4月份家务劳动32.5小时,5月份可得到的费用为250元.
点评:本题考查识图能力,也考查了利用待定系数法求一次函数关系式,正确理解题意比较关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目