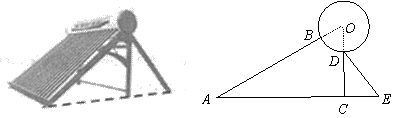题目内容
如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管与支架CD所在直线相交于水箱横断面⊙O的圆心O,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=76厘米,∠CED=60°.(1)求垂直支架CD的长度;(结果保留根号)
(2)求水箱半径OD的长度.(结果保留三个有效数字,参考数据:
| 2 |
| 3 |
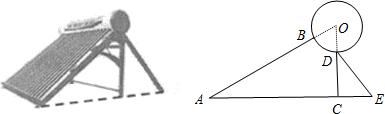
分析:(1)首先弄清题意,了解每条线段的长度与线段之间的关系,在△CDE中利用三角函数sin60°=
,求出CD的长.
(2)首先设出水箱半径OD的长度为x厘米,表示出CO,AO的长度,根据直角三角形的性质得到CO=
AO,再代入数计算即可得到答案.
| CD |
| DE |
(2)首先设出水箱半径OD的长度为x厘米,表示出CO,AO的长度,根据直角三角形的性质得到CO=
| 1 |
| 2 |
解答:解:(1)∵DE=76厘米,∠CED=60°,
∴sin60°=
=
,
∴CD=38
cm.
(2)设水箱半径OD的长度为x厘米,则CO=(38
+x)厘米,AO=(150+x)厘米,
∵∠BAC=30°,
∴CO=
AO,
38
+x=
(150+x),
解得:x=150-76
=150-131.48≈18.5cm.
∴sin60°=
| CD |
| DE |
| CD |
| 76 |
∴CD=38
| 3 |
(2)设水箱半径OD的长度为x厘米,则CO=(38
| 3 |
∵∠BAC=30°,
∴CO=
| 1 |
| 2 |
38
| 3 |
| 1 |
| 2 |
解得:x=150-76
| 3 |
点评:此题主要考查了解直角三角形的应用,充分体现了数学与实际生活的密切联系,做题的关键是表示出线段的长后,理清线段之间的关系.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 与支架
与支架 所在直线相交于水箱横断面
所在直线相交于水箱横断面 的圆心
的圆心 ,支架
,支架 垂直,
垂直, 厘米,
厘米, ,另一根辅助支架
,另一根辅助支架 厘米,
厘米, .
. 的长度.(结果保留三个有效数字,参考数据:
的长度.(结果保留三个有效数字,参考数据: )
)

 与支架
与支架 所在直线相交于水箱横断面
所在直线相交于水箱横断面 的圆心
的圆心 ,支架
,支架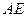 垂直,
垂直,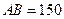 厘米,
厘米,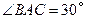 ,另一根辅助支架
,另一根辅助支架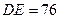 厘米,
厘米,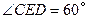 .
.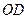 的长度.(结果保留三个有效数字,参考数据:
的长度.(结果保留三个有效数字,参考数据: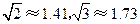 )
)
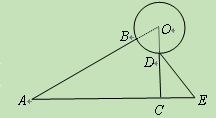
 O的圆心O,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=76厘米,∠CED=60°。
O的圆心O,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=76厘米,∠CED=60°。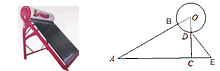
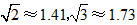 )
)