题目内容
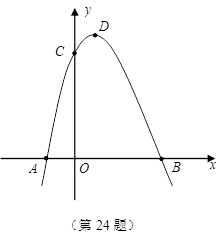
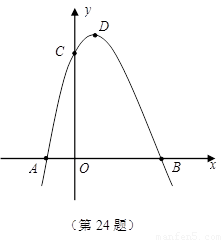
如图,抛物线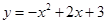 与
与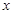 轴相交于
轴相交于 、
、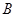 两点(点
两点(点 在点
在点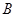 的左侧),与
的左侧),与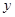 轴相交于点
轴相交于点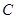 ,顶点为
,顶点为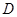 .
.

1.直接写出 、
、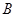 、
、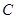 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;
2.连接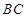 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点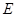 ,点
,点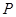 为线段
为线段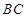 上的一个动点,过点
上的一个动点,过点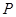 作
作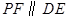 交抛物线于点
交抛物线于点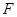 ,设点
,设点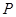 的横坐标为
的横坐标为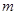 ;
;
①用含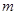 的代数式表示线段
的代数式表示线段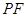 的长,并求出当
的长,并求出当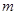 为何值时,四边形
为何值时,四边形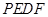 为平行四边形?
为平行四边形?
②设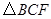 的面积为
的面积为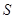 ,求
,求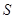 与
与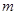 的函数关系式.
的函数关系式.
【答案】
1.A(-1,0),B(3,0),C(0,3).抛物线的对称轴是:x=1.
2.①设直线BC的函数关系式为:y=kx+b.把B(3,0),C(0,3)分别代入得:
 解得:k= -1,b=3.
解得:k= -1,b=3.
所以直线BC的函数关系式为: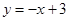 .当x=1时,y= -1+3=2,∴E(1,2).
.当x=1时,y= -1+3=2,∴E(1,2).
当 时,
时, ,
,
∴P(m,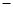 m+3).在
m+3).在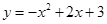 中,当
中,当 时,
时,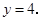 ∴
∴
当 时,
时,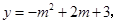 ∴
∴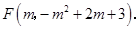
∴线段DE=4-2=2,线段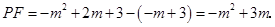 ∵
∵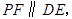
∴当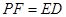 时,四边形
时,四边形 为平行四边形.由
为平行四边形.由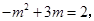 解得:
解得: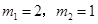 (不合题意,舍去).因此,当
(不合题意,舍去).因此,当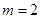 时,四边形
时,四边形 为平行四边形.
为平行四边形.
②设直线 与
与 轴交于点
轴交于点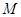 ,由
,由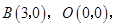 可得:
可得: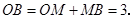
∵ 即
即 .
.

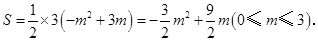
【解析】当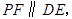
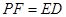 即一组对边平行且相等时四边形
即一组对边平行且相等时四边形 为平行四边形,从而可以求得
为平行四边形,从而可以求得 。
。

练习册系列答案
相关题目
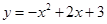 与
与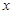 轴相交于
轴相交于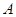 、
、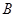 两点(点
两点(点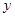 轴相交于点
轴相交于点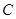 ,顶点为
,顶点为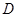 .
.
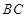 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点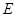 ,点
,点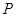 为线段
为线段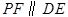 交抛物线于点
交抛物线于点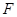 ,设点
,设点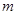 ;
;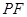 的长,并求出当
的长,并求出当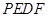 为平行四边形?
为平行四边形?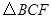 的面积为
的面积为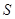 ,求
,求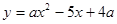 与
与 轴相交于点
轴相交于点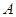 、
、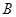 ,且经过点
,且经过点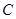 (5,4).该抛物线顶点为
(5,4).该抛物线顶点为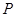 .
.
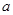 的值和该抛物线顶点
的值和该抛物线顶点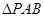 的面积;
的面积;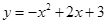 与
与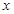 轴相交于
轴相交于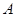 、
、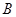 两点(点
两点(点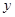 轴相交于点
轴相交于点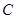 ,顶点为
,顶点为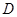 .
.
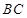 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点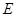 ,点
,点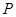 为线段
为线段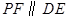 交抛物线于点
交抛物线于点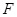 ,设点
,设点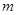 ;
;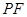 的长,并求出当
的长,并求出当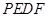 为平行四边形?
为平行四边形?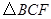 的面积为
的面积为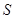 ,求
,求