题目内容
 29、如图,已知点D、E为△ABC的边BC上两点.AD=AE,BD=CE,为了判断∠B与∠C的大小关系,请你填空完成下面的推理过程,并在空白括号内注明推理的依据.
29、如图,已知点D、E为△ABC的边BC上两点.AD=AE,BD=CE,为了判断∠B与∠C的大小关系,请你填空完成下面的推理过程,并在空白括号内注明推理的依据.解:过点A作AH⊥BC,垂足为H.
∵在△ADE中,AD=AE(已知)
AH⊥BC(所作)
∴DH=EH(等腰三角形底边上的高也是底边上的中线)
又∵BD=CE(已知)
∴BD+DH=CE+EH(等式的性质)
即:BH=
CH
又∵
AH⊥BC
(所作)∴AH为线段
BC
的垂直平分线∴AB=AC(线段垂直平分线上的点到线段两个端点的距离相等)
∴
∠B=∠C
(等边对等角)分析:首先根据等腰三角形的性质,得DH=EH,结合已知条件,根据等式的性质,得BH=CH,从而根据线段垂直平分线的性质,得AB=AC,再根据等腰三角形的性质即可证明.
解答:解:过点A作AH⊥BC,垂足为H.
∵在△ADE中,AD=AE(已知),
AH⊥BC(所作),
∴DH=EH(等腰三角形底边上的高也是底边上的中线).
又∵BD=CE(已知),
∴BD+DH=CE+EH(等式的性质),
即:BH=CH.
又∵AH⊥BC(所作),
∴AH为线段BC的垂直平分线.
∴AB=AC(线段垂直平分线上的点到线段两个端点的距离相等).
∴∠B=∠C(等边对等角).
∵在△ADE中,AD=AE(已知),
AH⊥BC(所作),
∴DH=EH(等腰三角形底边上的高也是底边上的中线).
又∵BD=CE(已知),
∴BD+DH=CE+EH(等式的性质),
即:BH=CH.
又∵AH⊥BC(所作),
∴AH为线段BC的垂直平分线.
∴AB=AC(线段垂直平分线上的点到线段两个端点的距离相等).
∴∠B=∠C(等边对等角).
点评:此题综合运用了等腰三角形的性质、线段垂直平分线的性质.
等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合;等腰三角形的两个底角相等.
等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合;等腰三角形的两个底角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
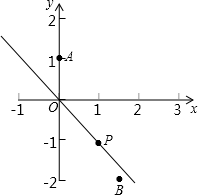 如图,已知点A的坐标为(0,1),点B的坐标为(
如图,已知点A的坐标为(0,1),点B的坐标为(| 3 |
| 2 |
| A、(2,-2) | ||||
| B、(4,-4) | ||||
C、(
| ||||
| D、(5,-5) |
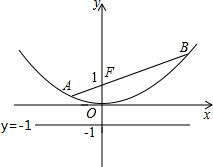 如图,已知点F的坐标为(0,1),过点F作一条直线与抛物线y=
如图,已知点F的坐标为(0,1),过点F作一条直线与抛物线y=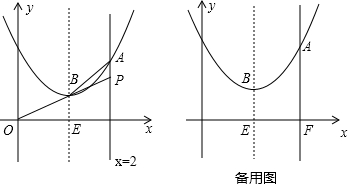
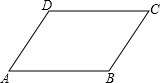 如图,已知点E在面积为4的平行四边形ABCD的边上运动,使△ABE的面积为1的点E共有
如图,已知点E在面积为4的平行四边形ABCD的边上运动,使△ABE的面积为1的点E共有 如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-
如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-