题目内容
已知mn≠1,且5m2+2009m+9=0,9n2+2009n+5=0,则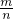 的值为
的值为
- A.-402
- B.
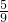
- C.
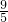
- D.
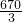
C
分析:将原题第二个等式左右两边同时除以n2,变形后与第一个等式比较,得到m与 为方程5x2+2009x+9=0的两个解,利用一元二次方程根与系数的关系即可求出所求式子的值.
为方程5x2+2009x+9=0的两个解,利用一元二次方程根与系数的关系即可求出所求式子的值.
解答:将9n2+2009n+5=0变形得:5×( )2+2009×
)2+2009× +9=0,
+9=0,
又5m2+2009m+9=0,
∴m与 为方程5x2+2009x+9=0的两个解,
为方程5x2+2009x+9=0的两个解,
则m• =
=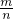 =
=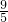 .
.
故选C
点评:此题考查了根与系数的关系,一元二次方程ax2+bx+c=0(a≠0),当方程有解,即b2-4ac≥0时,设方程两根分别为x1,x2,则有x1+x2=- ,x1x2=
,x1x2= .
.
分析:将原题第二个等式左右两边同时除以n2,变形后与第一个等式比较,得到m与
 为方程5x2+2009x+9=0的两个解,利用一元二次方程根与系数的关系即可求出所求式子的值.
为方程5x2+2009x+9=0的两个解,利用一元二次方程根与系数的关系即可求出所求式子的值.解答:将9n2+2009n+5=0变形得:5×(
 )2+2009×
)2+2009× +9=0,
+9=0,又5m2+2009m+9=0,
∴m与
 为方程5x2+2009x+9=0的两个解,
为方程5x2+2009x+9=0的两个解,则m•
 =
=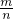 =
=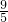 .
.故选C
点评:此题考查了根与系数的关系,一元二次方程ax2+bx+c=0(a≠0),当方程有解,即b2-4ac≥0时,设方程两根分别为x1,x2,则有x1+x2=-
 ,x1x2=
,x1x2= .
. 
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
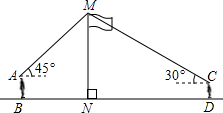 如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部M的仰角为30度.两人相距28米且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.(参考数据:
如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部M的仰角为30度.两人相距28米且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.(参考数据: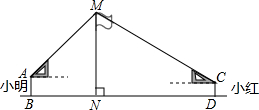 (2013•兰州)如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据:
(2013•兰州)如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: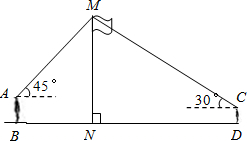 (2012•高邮市二模)如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(45°)是1.5m,看旗杆顶部M的仰角为30°.两人相距23m且位于旗杆两侧(点B,N,D)在同一条直线上).请求出旗杆MN的高度.(参考数据:
(2012•高邮市二模)如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(45°)是1.5m,看旗杆顶部M的仰角为30°.两人相距23m且位于旗杆两侧(点B,N,D)在同一条直线上).请求出旗杆MN的高度.(参考数据: ≈1.4,
≈1.4, ≈1.7,结果保留整数。)
≈1.7,结果保留整数。)