题目内容
矩形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置.点A1,A2,A3,A4…和点C1,C2,C3,C4…,分别在直线 (k>0)和x轴上,若点B1(1,2),B2(3,4),且满足
(k>0)和x轴上,若点B1(1,2),B2(3,4),且满足 ,则直线
,则直线 的解析式为 ,点
的解析式为 ,点 的坐标为 ,点
的坐标为 ,点 的坐标为_ .
的坐标为_ .
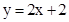 ;(7,8);(
;(7,8);(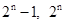 ).
).
解析试题分析:∵B1(1,2),B2(3,4),∴A1(0,2),A2(1,4).
∵A1,A2在直线 (k>0)上,∴
(k>0)上,∴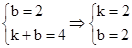 .
.
∴直线 的解析式为
的解析式为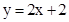 .
.
∵A3的横坐标与B2的横坐标相同,为3,且A3在直线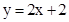 上,∴A3(3,8).
上,∴A3(3,8).
∵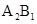 ∥
∥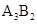 ,
, ,∴
,∴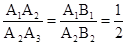 .
.
∵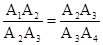 ,∴
,∴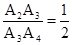 .
.
∴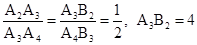 ,∴
,∴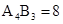 .∴
.∴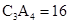 .
.
∵A4在直线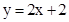 上,∴
上,∴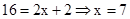 .∴B3(7,8).
.∴B3(7,8).
同理,可得B4(15,16),B5(31,32),…
可见:Bn(n=1,2,…)的横坐标为1,3,7,15,31,…,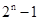 ;
;
Bn(n=1,2,…)的纵坐标为2,4,8,16,32,…,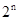 .
.
∴Bn(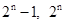 ).
).
考点:1.探索规律题(图形的变化类);2.一次函数图象上点的坐标特征;3.矩形的性质.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目

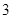 (填“>”“<”或“=”).
(填“>”“<”或“=”). .
.
 +
+ =0,则x+y= 。
=0,则x+y= 。