题目内容
关于x的一元函数y=-2x+m和反比例函数y=| n+1 | x |
(1)求一次函数和反比例函数的解析式;
(2)求一次函数与反比例函数的另一个交点B的坐标;
(3)求△AOB的面积.
分析:(1)把A的坐标代入两个函数的解析式中就可以确定两个函数的解析式;
(2)利用两个函数的解析式组成方程组,然后解方程组就可以确定另一个交点的坐标;
(3)先确定直线与x轴的交点C的坐标,然后用面积的割补法求△AOB的面积.
(2)利用两个函数的解析式组成方程组,然后解方程组就可以确定另一个交点的坐标;
(3)先确定直线与x轴的交点C的坐标,然后用面积的割补法求△AOB的面积.
解答: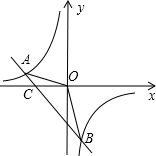 解:(1)把A(-2,1)代入函数关系式得到m=-3,n=-3
解:(1)把A(-2,1)代入函数关系式得到m=-3,n=-3
∴一次函数的解析式为y=-2x-3,反比例函数的解析式为y=-
;
(2)解方程组
,得:
,
,
∴B的坐标为(
,-4);
(3)∵一次函数的解析式为y=-2x-3,
∴y=0时,x=-
,则CO=
,
∴S△AOB=S△AOC+S△BOC=
×
×4+
×
×1=
.
 解:(1)把A(-2,1)代入函数关系式得到m=-3,n=-3
解:(1)把A(-2,1)代入函数关系式得到m=-3,n=-3∴一次函数的解析式为y=-2x-3,反比例函数的解析式为y=-
| 2 |
| x |
(2)解方程组
|
|
|
∴B的坐标为(
| 1 |
| 2 |
(3)∵一次函数的解析式为y=-2x-3,
∴y=0时,x=-
| 3 |
| 2 |
| 3 |
| 2 |
∴S△AOB=S△AOC+S△BOC=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 15 |
| 4 |
点评:此题首先利用待定系数法确定函数的解析式,然后利用函数解析式组成方程组去确定另一个交点的坐标,最后利用坐标表示线段长,表示不规则图形的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•丰台区二模)已知关于x的一元二次方程x2-4x+2(k-1)=0有两个不相等的实数根.
(2012•丰台区二模)已知关于x的一元二次方程x2-4x+2(k-1)=0有两个不相等的实数根.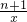 的图象都经过点A(-2,1).
的图象都经过点A(-2,1). 的图象都经过点A(-2,1).
的图象都经过点A(-2,1). 的图象都经过点A(-2,1).
的图象都经过点A(-2,1).