题目内容
以定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD, 以AF为边作正方形AMEF,点M在AD上(AM>MD),如图所示.
以AF为边作正方形AMEF,点M在AD上(AM>MD),如图所示.
(1)求证:M是线段AD的黄金分割点.
(2)如果AB=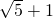 ,求AM的长.
,求AM的长.
(3)作PN⊥PD交BC于N连ND.△BPN与△PDN是否相似.若相似,证明你的结论;若不相似,请说明理由.
(1)证明:设PA=a,
∵P是AB的中点,
∴AB=2AP=2a,
∵四边形ABCD是正方形,
∴∠PAD=90°,AD=AB=2a,
在Rt△PAD中,PD=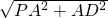 =
= a,
a,
∵PF=PD= a,
a,
∴FA=PF-PA= a-a=(
a-a=( -1)a,
-1)a,
∵四边形AMEF是正方形,
∴AM=AF=( -1)a,
-1)a,
∴ ,
,
∴M是线段AD的黄金分割点.
(2)解:由(1)知:PA= AB=
AB=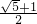 ,
,
∴AM=( -1)•PA=(
-1)•PA=( -1)×
-1)×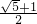 =2;
=2;
(3)解:△BPN与△PDN相似.
理由:∵PN⊥PD,
∴∠1+∠2=90°,∠DPN=90°,
∵四边形ABCD是正方形,
∴∠B=∠C=∠ADC=∠PAD=90°,AD=AB=BC=CD,
∴∠1+∠3=90°,
∴∠3=∠2,
∴△APD∽△BNP,
∴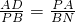 ,
,
∵AP= AB,
AB,
∴BN= BC,
BC,
设BN=x,则CN=3x,AD=AB=BC=CD=4x,AP=BP=2x,
∴在Rt△PAD中,PD=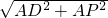 =
=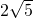 x,
x,
同理:PN= x,
x,
∴ ,
,
∴△BPN∽△PDN.
分析:(1)首先设PA=a,由正方形的性质与勾股定理,即可求得PD的长,又由PF=PD,即可求得FA的长,根据正方形的四边都相等,即可求得AM的值,再求AM与AD的比值,即可证得答案的正确性;
(2)根据(1)中的知识,求得PA的值,代入求解即可求得答案;
(3)首先利用有两角对应相等的三角形相似,证得△APD∽△BNP,根据相似三角形的对应边成比例,即可求得
2BN=PB,设BN=x,利用勾股定理求得PN与PD的长,即可求得 ,由对应边成比例且夹角相等的三角形相似,即可证得△BPN∽△PDN.
,由对应边成比例且夹角相等的三角形相似,即可证得△BPN∽△PDN.
点评:此题考查了正方形的性质,黄金分割的知识以及相似三角形的判定与性质等知识.此题综合性很强,难度适中,注意数形结合思想的应用.
∵P是AB的中点,
∴AB=2AP=2a,
∵四边形ABCD是正方形,
∴∠PAD=90°,AD=AB=2a,
在Rt△PAD中,PD=
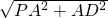 =
= a,
a,∵PF=PD=
 a,
a,∴FA=PF-PA=
 a-a=(
a-a=( -1)a,
-1)a,∵四边形AMEF是正方形,
∴AM=AF=(
 -1)a,
-1)a,∴
 ,
,∴M是线段AD的黄金分割点.
(2)解:由(1)知:PA=
 AB=
AB=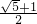 ,
,∴AM=(
 -1)•PA=(
-1)•PA=( -1)×
-1)×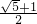 =2;
=2;(3)解:△BPN与△PDN相似.
理由:∵PN⊥PD,

∴∠1+∠2=90°,∠DPN=90°,
∵四边形ABCD是正方形,
∴∠B=∠C=∠ADC=∠PAD=90°,AD=AB=BC=CD,
∴∠1+∠3=90°,
∴∠3=∠2,
∴△APD∽△BNP,
∴
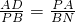 ,
,∵AP=
 AB,
AB,∴BN=
 BC,
BC,设BN=x,则CN=3x,AD=AB=BC=CD=4x,AP=BP=2x,
∴在Rt△PAD中,PD=
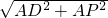 =
=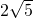 x,
x,同理:PN=
 x,
x,∴
 ,
,∴△BPN∽△PDN.
分析:(1)首先设PA=a,由正方形的性质与勾股定理,即可求得PD的长,又由PF=PD,即可求得FA的长,根据正方形的四边都相等,即可求得AM的值,再求AM与AD的比值,即可证得答案的正确性;
(2)根据(1)中的知识,求得PA的值,代入求解即可求得答案;
(3)首先利用有两角对应相等的三角形相似,证得△APD∽△BNP,根据相似三角形的对应边成比例,即可求得
2BN=PB,设BN=x,利用勾股定理求得PN与PD的长,即可求得
 ,由对应边成比例且夹角相等的三角形相似,即可证得△BPN∽△PDN.
,由对应边成比例且夹角相等的三角形相似,即可证得△BPN∽△PDN.点评:此题考查了正方形的性质,黄金分割的知识以及相似三角形的判定与性质等知识.此题综合性很强,难度适中,注意数形结合思想的应用.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
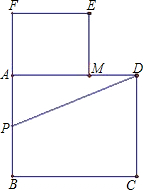 以AF为边作正方形AMEF,点M在AD上(AM>MD),如图所示.
以AF为边作正方形AMEF,点M在AD上(AM>MD),如图所示.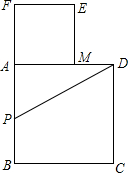 F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.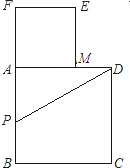 如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.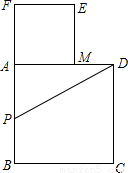 F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.