题目内容
（2013•瑶海区一模）将一副三角板按如图叠放，若OB=| 3 |
3
3
．分析：根据题意得HO，BH的长，进而得出BC的长以及BD的长，即可得出DO的长．
解答：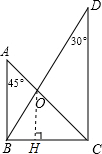
解：过点O作OH⊥BC于点H，
由题意可得：∠OBH=60°，
则sin60°=
=
=
，
解得：OH=
，
由BO=
，可得BH=
，
∵∠A=∠ACB=45°，
∴HC=HO=
，
∴BC=
+
，
∵∠D=30°，
∴BD=2BC=3+
，
∴DO=BC-BO=3+
-
=3．
故答案为：3．
解：过点O作OH⊥BC于点H，由题意可得：∠OBH=60°，
则sin60°=
| OH |
| BO |
| ||
| 2 |
| OH | ||
|
解得：OH=
| 3 |
| 2 |
由BO=
| 3 |
| ||
| 2 |
∵∠A=∠ACB=45°，
∴HC=HO=
| 3 |
| 2 |
∴BC=
| 3 |
| 2 |
| ||
| 2 |
∵∠D=30°，
∴BD=2BC=3+
| 3 |
∴DO=BC-BO=3+
| 3 |
| 3 |
故答案为：3．
点评：本题考查了相似三角形的判定和性质以及解直角三角形，利用锐角三角函数的应用求出BC的长是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
（2013•瑶海区一模）如图，已知A是反比例函数
（2013•瑶海区一模）如图，梯形ABCD中，AD∥BC，E是CD的中点，EA⊥AB，且AB=8，AE=6，则梯形ABCD的面积等于（ ）