题目内容
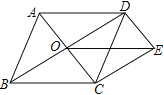
如图,□ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE= AC,连接CE、OE
AC,连接CE、OE
(1)求证:四边形OCED是平行四边形;
(2)若AD=DC=3,求OE的长.
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
题目内容
如图,□ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE= AC,连接CE、OE
AC,连接CE、OE
(1)求证:四边形OCED是平行四边形;
(2)若AD=DC=3,求OE的长.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案