题目内容
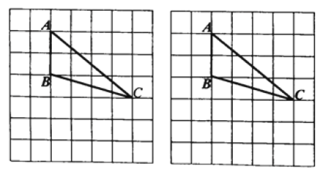
【题目】如图,等腰直角三角形ABC中,∠ABC=90°,BA=BC,将BC绕点B顺时针旋转θ(0°<θ<90°),得到BP,连结CP,过点A作AH⊥CP交CP的延长线于点H,连结AP,则∠PAH的度数( )
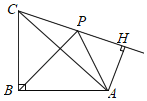
A.随着θ的增大而增大
B.随着θ的增大而减小
C.不变
D.随着θ的增大,先增大后减小
【答案】C
【解析】
由旋转的性质可得BC=BP=BA,由等腰三角形的性质和三角形内角和定理可求∠BPC+∠BPA=135°=∠CPA,由外角的性质可求∠PAH=135°﹣90°=45°,即可求解.
解:∵将BC绕点B顺时针旋转θ(0°<θ<90°),得到BP,
∴BC=BP=BA,
∴∠BCP=∠BPC,∠BPA=∠BAP,
∵∠CBP+∠BCP+∠BPC=180°,∠ABP+∠BAP+∠BPA=180°,∠ABP+∠CBP=90°,
∴∠BPC+∠BPA=135°=∠CPA,
∵∠CPA=∠AHC+∠PAH=135°,
∴∠PAH=135°﹣90°=45°,
∴∠PAH的度数是定值,
故选:C.

练习册系列答案
相关题目
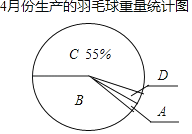
【题目】一只羽毛球的重量合格标准是5.0克~5.2克(含5.0克,不含5.2克),某厂对4月份生产的羽毛球重量进行抽样检验.并将所得数据绘制成如图统计图表.
4月份生产的羽毛球重量统计表
组别 | 重量x(克) | 数量(只) |
A | x<5.0 | m |
B | 5.0≤x<5.1 | 400 |
C | 5.1≤x<5.2 | 550 |
D | x≥5.2 | 30 |
(1)求表中m的值及图中B组扇形的圆心角的度数.
(2)问这些抽样检验的羽毛球中,合格率是多少?如果购得4月份生产的羽毛球10筒(每筒12只),估计所购得的羽毛球中,非合格品的羽毛球有多少只?