��Ŀ����
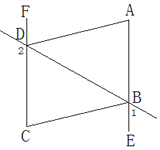
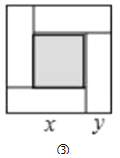
����Ŀ����ͼ��ʾ,���ĸ�ͬ����С��ֱ��������,����ֱ�DZ߷ֱ�Ϊa,b,б��Ϊc,ƴ��һ��������,�м�����һ��С������.
��1����������֮��������ϵ,̽��������a,b,c�ĵ�ʽ.
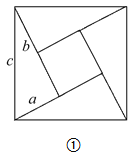
��2�����ã�1���з��ֵ�ֱ������������ֱ�DZ�a,b��б��c֮��Ĺ�ϵ���������:��ͼ����ֱ����ABC�У���C=90������c=6��a+b=8������ABC�����Ϊ__________
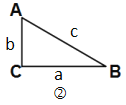
��3����ͼ�ۣ��������εı߳�Ϊm��С�����εı߳�Ϊn������x��y��ʾ�ĸ����ε����߳���x��y�����۲�ͼ����ָ�����¹�ϵʽ��
��1��![]() ��2��x+y=m ��3��x2��y2=mn
��2��x+y=m ��3��x2��y2=mn
��4��![]() ������ȷ����_________������ţ�
������ȷ����_________������ţ�
���𰸡�(1)a2+b2=c2��(2) 7����3��������ȷ����(1)(2)(3)(4)
�������������������1��������ABCD�������ȥ4�������ε�����ɵ�a2+b2=c2��
��2��Ҫ��Rt��ABC�������ֻ���������ֱ�DZߵij˻������ݹ��ɶ�������a2+b2=c2=36�����ݹ��ɶ����Ϳ������ab��ֵ�������õ������ε������
��3�����ô������εı߳�=�����εij�+�����εĿ���С�����εı߳�=�����εij�һ�����εĿ����������ε����һС�����ε����=4�������ε�����ж����ɣ�
�����������1��S������=(a+b)24��![]() ab��a2+b2= c2��
ab��a2+b2= c2��
��2����a2+b2=c2=36��
2ab=��a+b��2-��a2+b2��=82-62=28��
��ab=14��
��S��ABC=![]() ab=
ab=![]() ��14=7��
��14=7��
(3) ��m2-n2=4xy�������ȷ��
��x+y=m�������ȷ��
��x2-y2=��x+y����x-y��=mn��������ȷ��
��x2+y2=��x+y��2-2xy=m2-2��![]() =
=![]() ��������ȷ��
��������ȷ��

 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�