题目内容
(2013•沁阳市一模)以原点为圆心,1cm为半径的圆分别交x、y轴的正半轴于A、B两点,点P的坐标为(2,0).
(1)如图1,动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设经过的时间为t秒,当t=1时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留);
(2)若点Q按照(1)中的方向和速度继续运动,
①当t为何值时,以O、P、Q为顶点的三角形是直角三角形;
②在①的条件下,如果直线PQ与⊙O相交,请求出直线PQ被⊙O所截的弦长.
(1)如图1,动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设经过的时间为t秒,当t=1时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留);
(2)若点Q按照(1)中的方向和速度继续运动,
①当t为何值时,以O、P、Q为顶点的三角形是直角三角形;
②在①的条件下,如果直线PQ与⊙O相交,请求出直线PQ被⊙O所截的弦长.

分析:(1)连接OQ,求出∠QPO,求出∠BOQ,根据弧长公式求出即可;
(2)分为四种情况,画出图形,求出弧长,即可求出答案;
(3)作OM⊥PQ,根据面积公式即可求出答案.
(2)分为四种情况,画出图形,求出弧长,即可求出答案;
(3)作OM⊥PQ,根据面积公式即可求出答案.
解答: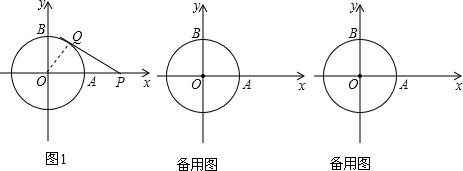 解:(1)如图1,连接OQ,则OQ⊥PQ.
解:(1)如图1,连接OQ,则OQ⊥PQ.
∵OQ=OA=1,OP=2,
∴∠QPO=30°,
∵∠PQO=90°,
∴∠QOP=60°,
∴∠BOQ=30°,
∴弧BQ的长是
=
π,
∵运动时间t=1,
 ∴点Q的运动速度为
∴点Q的运动速度为
π;
(2)分为四种情况:①由(1)可知,当t=1时,△OPQ为直角三角形;
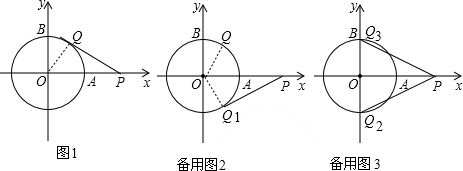
②如图2,当点Q1关于x轴对称时,
△OPQ1为直角三角形,此时∠BOQ1=150°,
弧BQ1=
π,T=5;
③当点Q2(0,-1)或Q3(0,1)时,∠POQ2=∠POQ3=90°,此时t=6或t=12
 即当t=1,t=5,t=6或t=12时,△OPQ为直角三角形;
即当t=1,t=5,t=6或t=12时,△OPQ为直角三角形;
(3)如图3,当t=6或t=12时,直线PQ与⊙O相交,设交点为N,
作OM⊥PQ,根据等面积法可知:PQ•OM=OQ•OP,
PQ=
=
,OM=
,
QM=
=
,
弦长QN=2QM=
CM.
 解:(1)如图1,连接OQ,则OQ⊥PQ.
解:(1)如图1,连接OQ,则OQ⊥PQ.∵OQ=OA=1,OP=2,
∴∠QPO=30°,
∵∠PQO=90°,
∴∠QOP=60°,
∴∠BOQ=30°,
∴弧BQ的长是
| 30π×1 |
| 180 |
| 1 |
| 6 |
∵运动时间t=1,
 ∴点Q的运动速度为
∴点Q的运动速度为| 1 |
| 6 |
(2)分为四种情况:①由(1)可知,当t=1时,△OPQ为直角三角形;
②如图2,当点Q1关于x轴对称时,
△OPQ1为直角三角形,此时∠BOQ1=150°,
弧BQ1=
| 5 |
| 6 |
③当点Q2(0,-1)或Q3(0,1)时,∠POQ2=∠POQ3=90°,此时t=6或t=12
 即当t=1,t=5,t=6或t=12时,△OPQ为直角三角形;
即当t=1,t=5,t=6或t=12时,△OPQ为直角三角形;(3)如图3,当t=6或t=12时,直线PQ与⊙O相交,设交点为N,
作OM⊥PQ,根据等面积法可知:PQ•OM=OQ•OP,
PQ=
| OP2+OQ2 |
| 5 |
2
| ||
| 5 |
QM=
| OQ2-OM2 |
| ||
| 5 |
弦长QN=2QM=
2
| ||
| 5 |
点评:本题考查了弧长的计算,三角形面积公式,切线的性质,含30度角的直角三角形性质等知识点的应用,主要考查学生的计算能力,用了分类讨论思想.

练习册系列答案
相关题目
 (2013•沁阳市一模)在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABO的三个顶点都在格点上.
(2013•沁阳市一模)在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABO的三个顶点都在格点上. (2013•沁阳市一模)如图,将半径为8的⊙O沿AB折叠,弧AB恰好经过与AB垂直的半径OC的中点D,则折痕AB长为( )
(2013•沁阳市一模)如图,将半径为8的⊙O沿AB折叠,弧AB恰好经过与AB垂直的半径OC的中点D,则折痕AB长为( )