题目内容
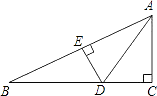
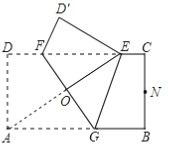
【题目】如图,矩形纸片ABCD中,AD=1,AB=2.将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.当△AED的外接圆与BC相切于BC的中点N.则折痕FG的长为______.
【答案】![]()
【解析】试题分析:设AE与FG的交点为O. 根据轴对称的性质,得AO=EO.
取AD的中点M,连接MO. 则MO=![]() DE,MO∥DC.
DE,MO∥DC.
设DE=x,则MO=![]() x, 在矩形ABCD中,∠C=∠D=90°,
x, 在矩形ABCD中,∠C=∠D=90°,
所以AE为△AED的外接圆的直径,O为圆心. 延长MO交BC于点N,则ON∥CD.
所以∠CNM=180°-∠C=90°. 所以ON⊥BC,四边形MNCD是矩形.
所以MN=CD=AB=2.所以ON=MN-MO=2-![]() x.
x.
因为△AED的外接圆与BC相切, 所以ON是△AED的外接圆的半径.
所以OE=ON=2-![]() x,AE=2ON=4-x.
x,AE=2ON=4-x.
根据Rt△AED的勾股定理可得:x=![]() 所以DE=
所以DE=![]() ,OE=2-
,OE=2-![]() x=
x=![]() .
.
根据轴对称的性质,得AE⊥FG. 所以∠FOE=∠D=90°.可得FO=![]() .
.
又AB∥CD,所以∠EFO=∠AGO,∠FEO=∠GAO. 所以△FEO≌△GAO.所以FO=GO.
所以FG=2FO=![]() 所以折痕FG的长是
所以折痕FG的长是![]() .
.

练习册系列答案
相关题目