Question

在复习课上，老师布置了一道思考题：如图所示，点M，N分别在等边△ABC的BC、CA边上，且BM=CN，AM、BN交于点Q，求证：∠BQM=60°．
（1）请你完成这道思考题；
（2）做完（1）后，同学们在老师的启发下进行了反思，提出许多问题，譬如：
①若将题中“BM=CN”与“∠BQM=60°”的位置交换，得到的是否仍是真命题？
②若将题中的点M，N分别移动到BC，CA的延长线上，是否仍能得到∠BQM=60°？请你选择其中一个问题并画出图形，给出证明．

Answer 1

分析：（1）由已知条件得△ABM≌△BCN，得∠BAM=∠CBN，又因为∠QBA+∠CBN=∠CBA=60°，所以∠QBA+∠BAM=60°，即有∠BQM=60°；
（2）①因为∠BQM=60°，所以∠QBA+∠BAM=60°，又因为∠QBA+∠CBN=60°，所以∠BAM=∠CBN，已知∠B=∠C，AB=AC，则ASA可判定△ABM≌△BCN，即BM=CN；②成立．

解答：解：（1）∵在△ABM和△BCN中，

BM=CN ∠B=∠C AB=BC

，
∴△ABM≌△BCN（SAS）．
∴∠BAM=∠CBN（全等三角形对应角相等）．
∵∠QBA+∠CBN=∠CBA=60°（已知），
∴∠QBA+∠BAM=60°（等量代换）．
∴∠BQM=60°．

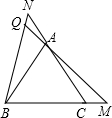（2）①是．
∵∠BQM=60°（已知），
∴∠QBA+∠BAM=60°．
∵∠QBA+∠CBN=60°（由（1）得出的结论），
∴∠BAM=∠CBN（等量代换）．
在△ABM和△BCN中，

∠ABM=∠BCN AB=AC ∠BAM=∠CBN

∴△ABM≌△BCN（ASA）．
∴BM=CN（全等三角形对应边相等）．
②成立．
∵BM=CN（①的结论），
∴CM=AN（等量代换）．
∵AB=AC，∠ACM=∠BAN=180°-60°=120°（平角的性质），
在△BAN和△ACM中，

BA=AC ∠BAN=∠ACM AN=CM

∴△BAN≌△ACM（SAS）．
∴∠NBA=∠MAC，
∴∠BQM=∠BNA+∠NAQ=180°-∠NCB-（∠CBN-∠NAQ）=180°-60°-60°=60°（三角形内角和定理）．

点评：本题考查了全等三角形的判定和性质及等边三角形的性质；此题把全等三角形的判定和性质结合求解．有利于培养学生综合运用数学知识的能力，全等三角形的证明是正确解答本题的关键．