题目内容
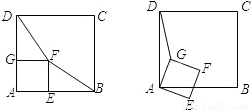
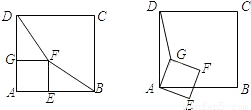
(2004•厦门)如图,正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.(1)连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题“在旋转的过程中,线段DF与BF的长始终相等”是否正确?若正确,请证明;若不正确,请举例说明;
(2)若将正方形AEFG绕点A按顺时针方向旋转,连接DG,在旋转过程中,你能否找到一条线段的长与线段DG的长始终相等?并以图为例说明理由.
【答案】分析:(1)显然,当A,F,B在同一直线上时,DF≠BF.
(2)注意使用两个正方形的边和90°的角,可判断出△DAG≌△BAE,那么DG=BE.
解答: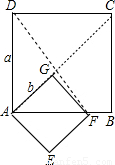 解:(1)不正确.
解:(1)不正确.
若在正方形GAEF绕点A顺时针旋转45°,这时点F落在线段AB或AB的延长线上.(或将正方形GAEF绕点A顺时针旋转,使得点F落在线段AB或AB的延长线上).如图:
设AD=a,AG=b,
则DF=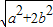 >a,
>a,
BF=|AB-AF|=|a-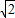 b|<a,
b|<a,
∴DF>BF,即此时DF≠BF;
(2)连接BE,可得△ADG≌△ABE,
则DG=BE.如图,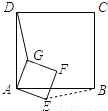
∵四边形ABCD是正方形,
∴AD=AB,
∵四边形GAEF是正方形,
∴AG=AE,
又∠DAG+∠GAB=90°,∠BAE+∠GAB=90°,
∴∠DAG=∠BAE,
∴△DAG≌△BAE,
∴DG=BE.
点评:注意点在特殊位置时所得到的关系,判断边相等,通常要找全等三角形.
(2)注意使用两个正方形的边和90°的角,可判断出△DAG≌△BAE,那么DG=BE.
解答:
 解:(1)不正确.
解:(1)不正确.若在正方形GAEF绕点A顺时针旋转45°,这时点F落在线段AB或AB的延长线上.(或将正方形GAEF绕点A顺时针旋转,使得点F落在线段AB或AB的延长线上).如图:
设AD=a,AG=b,
则DF=
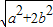 >a,
>a,BF=|AB-AF|=|a-
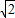 b|<a,
b|<a,∴DF>BF,即此时DF≠BF;
(2)连接BE,可得△ADG≌△ABE,
则DG=BE.如图,

∵四边形ABCD是正方形,
∴AD=AB,
∵四边形GAEF是正方形,
∴AG=AE,
又∠DAG+∠GAB=90°,∠BAE+∠GAB=90°,
∴∠DAG=∠BAE,
∴△DAG≌△BAE,
∴DG=BE.
点评:注意点在特殊位置时所得到的关系,判断边相等,通常要找全等三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目