��Ŀ����
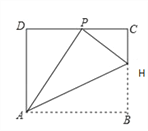
����Ŀ����ͼ��������ABCD��AH�۵���ʹ�ö���B����CD���ϵ�P�㴦���ۺ����BC���ڵ� H,
��֪AD=8��HC:HB=3:5.
��1����֤����HCP�ס�PDA��
��2�� ̽��AB��HB֮���������ϵ����֤����Ľ��ۣ�
��3������BP������M���߶�AP�ϣ���M���P��A���غϣ�������N���߶�AB���ӳ����ϣ���BN=PM������MN��PB�ڵ�F����ME��BP�ڵ�E�����ʵ���M��N���ƶ������У��߶�EF�ij����Ƿ����仯�����仯��˵�����ɣ�˵�����ɣ������䣬����߶�EF�ij��ȣ�
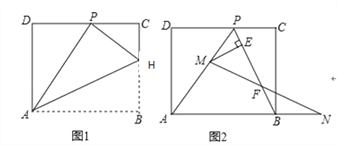
���𰸡���1��֤������������2��AB=2BH.�����ɼ�������(3) EF�ij��Ȳ��䣮
�������������������1���������Ƕ�Ӧ��ȵ������������ƿ���֤��
��2�����ݣ�1���Ľ��ۣ������������ε����ʿ��������֮��Ĺ�ϵ��
��3����MQ��AB��PB��Q���ɵ���MQP=��ABP�� Ȼ�����۵������ʿ�֪����APB=��ABP������MQP=��APB�����ݵȽǶԵȱ߿ɵ�MP=MQ����BN=PM�����ݵ��������ɵ�MQ=BN��Ȼ����ƽ���߷��߶γɱ�������EF=![]() PB�������ݹ��ɶ������.
PB�������ݹ��ɶ������.
�����������1�����۵������ʿ�֪��
��APH=��B=90�㣬 ���APD+��HPC=90�㣬
�֡�PHC+��HPC=90�㣬 ���APD=��PHC��
�֡�D=��C=90�㣬���HCP�ס�PDA��
��2��AB=2BH.
��HC:HB=3:5����HC=3x����HB=5x��
�ھ���ABCD�У�BC=AD=8 ����HC=3����HB=5
���۵������ʿ�֪HP=HB=5,AP=AB,
��Rt��HCP,��PC=4��
�ߡ�HCP�ס�PDA
��![]() ,��
,��![]()
��AB=AP=10=2BH,��AB=2BH.
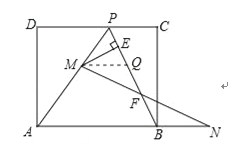
��3��EF�ij��Ȳ��䣮
��MQ��AB��PB��Q�� ���MQP=��ABP��
���۵������ʿ�֪����APB=��ABP��
���MQP=��APB��
��MP=MQ����BN=PM����MQ=BN��
��MQ��AB����![]() ��
��
��QF=FB��
��MP=MQ��ME��BP�� ��PE=QE����EF=![]() PB��
PB��
�ɣ�2���ã�PC=4��BC=8��
��PB=![]() =
=![]() ��
��
��EF=![]()