题目内容
 如图,A城气象台测得台风中心在A城正西方向160
如图,A城气象台测得台风中心在A城正西方向160| 2 |
| 2 |
(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风影响,那么A城遭受这次台风影响有多长的时间?
分析:(1)点到直线的线段中垂线段最短,故应由A点向BP作垂线,垂足为F,若AF>200km则A城不受影响,否则受影响;
(2)点A到直线BF的长为200千米的点有两点,分别设为D、G,则△ADG是等腰三角形,由于AF⊥BP,则P是DG的中点,
在Rt△ADF中,解出FD的长,则可求DG长,在DG长的范围内都是受台风影响,再根据速度与距离的关系则可求时间.
(2)点A到直线BF的长为200千米的点有两点,分别设为D、G,则△ADG是等腰三角形,由于AF⊥BP,则P是DG的中点,
在Rt△ADF中,解出FD的长,则可求DG长,在DG长的范围内都是受台风影响,再根据速度与距离的关系则可求时间.
解答: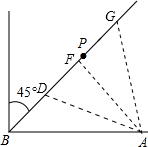 解:(1)由A点向BP作垂线,垂足为F,
解:(1)由A点向BP作垂线,垂足为F,
在Rt△ABF中,∠ABP=45°,AB=160
km,则AF=160km,
因为160km<200km,所以A城要受台风影响;
(2)设BP上点D,DA=200千米,则还有一点G,有
AG=200千米.
因为DA=AG,所以△ADG是等腰三角形,
因为AF⊥BP,所以AF是DG的垂直平分线,DF=FG,
在Rt△ADF中,DA=200千米,AF=160千米,
由勾股定理得,DF=
=120km,
∴则DG=2DC=240千米,
遭受台风影响的时间是:t=240÷40=6(小时).
 解:(1)由A点向BP作垂线,垂足为F,
解:(1)由A点向BP作垂线,垂足为F,在Rt△ABF中,∠ABP=45°,AB=160
| 2 |
因为160km<200km,所以A城要受台风影响;
(2)设BP上点D,DA=200千米,则还有一点G,有
AG=200千米.
因为DA=AG,所以△ADG是等腰三角形,
因为AF⊥BP,所以AF是DG的垂直平分线,DF=FG,
在Rt△ADF中,DA=200千米,AF=160千米,
由勾股定理得,DF=
| AD2-AF2 |
∴则DG=2DC=240千米,
遭受台风影响的时间是:t=240÷40=6(小时).
点评:此题主要考查辅助线在题目中的应用,勾股定理,点到直线的距离及速度与时间的关系等,较为复杂.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域. 如图,A城气象台测得台风中心在A城的正西方300千米处,以每小时10
如图,A城气象台测得台风中心在A城的正西方300千米处,以每小时10 如图,A城气象台测得台风中心在城正西方向300千米的B处,并以每小时10
如图,A城气象台测得台风中心在城正西方向300千米的B处,并以每小时10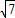 千米的速度向北偏东60°的BF方向移动,距台风中心200千米的范围内是受这次台风影响的区域.
千米的速度向北偏东60°的BF方向移动,距台风中心200千米的范围内是受这次台风影响的区域.