题目内容
【题目】一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
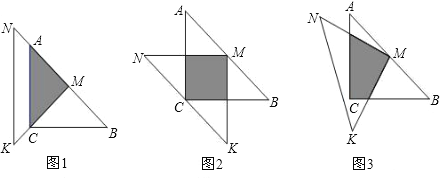
(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为 ,周长为 .
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为 ,周长为 .
2(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.
【答案】(1)重叠部分的面积是△ACB的面积的一半为a2,周长为(1+)a.(2)边长为a,面积为a2,周长为2a.(3)![]() .
.
【解析】解:(1)∵AM=MC=![]() AC=
AC=![]() a,则
a,则
∴重叠部分的面积是△ACB的面积的一半为a2,周长为(1+)a.
(2)∵重叠部分是正方形
∴边长为a,面积为a2,周长为2a.
(3)猜想:重叠部分的面积为![]() .
.
理由如下:
过点M分别作AC、BC的垂线MH、MG,垂足为H、G
设MN与AC的交点为E,MK与BC的交点为F
∵M是△ABC斜边AB的中点,AC=BC=a
∴MH=MG=![]()
又∵∠HME+∠HMF=∠GMF+∠HMF,
∴∠HME=∠GMF,
∴Rt△MHE≌Rt△MGF
∴阴影部分的面积等于正方形CGMH的面积
∵正方形CGMH的面积是MGMH=![]() ×
×![]() =
=![]()
∴阴影部分的面积是![]() .
.


练习册系列答案
相关题目