题目内容
随机抽取某市去年30天的空气污染指数(皆为整数),绘制了尚未完成的 频率分布表和频率分布直方图
频率分布表和频率分布直方图
| 分组 | 频数 | 频率 |
| 25.5~50.5 | 6 | |
| 50.5~75.5 | ||
| 75.5~l00.5 | 0.3 | |
| 100.5~125.5 | 3 | |
| 合计 | 30 | 1 |
(1)完成频率分布表及补全频率分布直方图;
(2)这组数据的中位数在哪个分组内?答:______.
(3)能否确定这组数据的众数在哪个分组内?答:______.
(4)若污染指数不大于50时,空气质量为优,试估计该市去年(按365天计算)空气质量达到优的天数,答:______天.
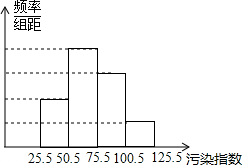 解:(1)由题意得:
解:(1)由题意得:频率:25.5~50.5的频率为:6÷30=0.2,
100.5~125.5的频率为:3÷30=0.1,
50.5~75.5的频率为:1-0.2-0.2-0.3=0.4,
50.5~75.5的频数为:30×0.4=12,
75.5~l00.5的频数为:30×0.3=9;
补全直方图为:
(2)∵第一组有6个数,第二组有12个数.
∴第一、二组有18个数.
∵中位数是第15和第16两个数的平均数,
∴中位数在50.5一75.5组内;
故答案为:50.5~75.5;
(3)众数一组数据中出现次数最多的数,根据条件无法判定;
故答案为:不能确定;
(4)由题意,得
365×(6÷30)=73(天)
故答案为:73.
分析:(1)由数据总数为30及第一组和第四组的频数就可以求出第一组的频率和第四组的频率,从而可以求出第二组的频率,进而可以求出第二组的频数;通过求出的频数就可以补全频数分布直方图;
(2)根据中位数的定义就可以求得是第15和第16的这两个数的平均数,由(1)可以求出结论;
(3)众数一组数据中出现次数最多的数,根据条件无法判定;
(4)计算30天空气为优所占的比率,然后乘以365就可以得出结论.
点评:本题考查了频数分布直方图的运用,频数分布表的运用,众数中位数的运用及根据样本数据估计总体数据得运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
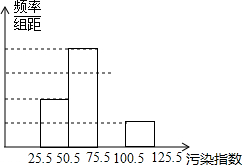 频率分布表和频率分布直方图
频率分布表和频率分布直方图