��Ŀ����
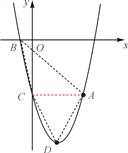
����Ŀ����ͼ1����ƽ��ֱ������ϵxOy�У���B����2��2����������������y=![]() ��x��0������k��0��ͼ����һ��A����
��x��0������k��0��ͼ����һ��A����![]() ��m����y���ƽ���߽�ֱ��l��y=x+2�ڵ�C����AC=AB��
��m����y���ƽ���߽�ֱ��l��y=x+2�ڵ�C����AC=AB��
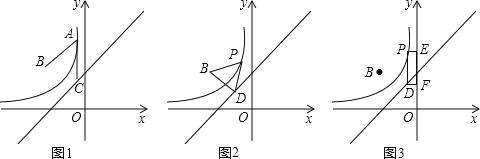
��1���ֱ����m��k��ֵ����д�������������������ʽ��
��2�����֣�������y=![]() ��x��0��ͼ��������һ��P����y���ƽ���߽�ֱ��l�ڵ�D����ֱ��д���㷢�ֵ�PB��PD��������ϵ ��
��x��0��ͼ��������һ��P����y���ƽ���߽�ֱ��l�ڵ�D����ֱ��д���㷢�ֵ�PB��PD��������ϵ ��
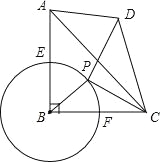
Ӧ�ã�����ͼ2������BD������PBD�ǵȱ�������ʱ�����ʱ��P�����ꣻ
����ͼ3���ֱ����P��D��y�Ĵ��߽�y���ڵ�E��F�����Ƿ���ڵ�P��ʹ�þ���PEFD���ܳ�ȡ����Сֵ�������ڣ��������ʱ��P�����꼰����PEFD���ܳ����������ڣ���˵�����ɣ�
���𰸡���1��y=��![]() ��x��0����2��PB=PD����1��
��x��0����2��PB=PD����1��![]() ��
��![]() +1���������ڣ�����1��2����4
+1���������ڣ�����1��2����4
��������
�����������1�����AC��AB�ı���ʽ������AC=AB���m��ֵ��Ȼ�����ô���ϵ�������k��ֵ���ɣ�
��2����P����m��![]() ����m��0������D����m����m+2�������ݹ��ɶ������PB�ij����ɣ�������PBD�ǵȱ������Σ����ǵõ�PB=BD=PD�����ݵȱ������ε����ʵõ���2��m��=
����m��0������D����m����m+2�������ݹ��ɶ������PB�ij����ɣ�������PBD�ǵȱ������Σ����ǵõ�PB=BD=PD�����ݵȱ������ε����ʵõ���2��m��=![]() ��
��![]() +m��2����ã�m=3��
+m��2����ã�m=3��![]() ����m=
����m=![]() ��1�����ǵõ�P��
��1�����ǵõ�P��![]() ��3��
��3��![]() ����P��1��
����P��1��![]() ��
��![]() +1�����ڸ��ݾ��ε��ܳ��ļ��㹫ʽ�õ�����PEFD���ܳ�=��
+1�����ڸ��ݾ��ε��ܳ��ļ��㹫ʽ�õ�����PEFD���ܳ�=��![]() ��
��![]() ��2+4�����ݶ��κ��������ʼ��ɵõ����ۣ�
��2+4�����ݶ��κ��������ʼ��ɵõ����ۣ�
�����������1��AC=m��![]() ��AB=
��AB=![]() ��
��
��AC=AF��
��m=4��
����A����![]() ��4����
��4����
��k=��2��
��y=��![]() ��x��0����
��x��0����
��2����P����m��![]() ����m��0������D��m��m+2����
����m��0������D��m��m+2����
��PD=![]() ������m+2��=
������m+2��=![]() +m��2��
+m��2��
BP=![]() =
=![]() +m��2��
+m��2��
��PD=PB��
�ʴ�Ϊ��PB=PD��
���ߡ�PBD�ǵȱ������Σ�
��PB=BD=PD��
��PD��y�ᣬ
����2��m��=![]() ��
��![]() +m��2��
+m��2��
��![]() +m��2=
+m��2=![]() ��
��
��m=3��![]() ����m=
����m=![]() ��1��
��1��
��P��1��![]() ��
��![]() +1����
+1����
�ڴ𣺴����������������ĵ�P��
��P����m��![]() ����m��0������D����m����m+2����
����m��0������D����m����m+2����
������PEFD���ܳ�=2��PD+PE��=2��![]() +m��2+m��=
+m��2+m��=![]() +4m��4=��
+4m��4=��![]() ��
��![]() ��2+4��
��2+4��
����![]() ��
��![]() =0����m=2ʱ��P����1��2��ʱ������PEFD���ܳ�ȡ����СֵΪ4��
=0����m=2ʱ��P����1��2��ʱ������PEFD���ܳ�ȡ����СֵΪ4��

 �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д� �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д�