题目内容
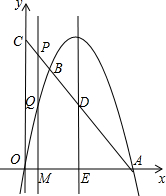 如图,点A是抛物线
如图,点A是抛物线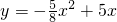 与x轴正半轴的交点,点B在这条抛物线上,且点B的横坐标为2.连接AB并延长交y轴于点C,抛物线的对称轴交AC于点D,交x轴于点E.点P在线段CA上,过点P作x轴的垂线,垂足为点M,交抛物线于点Q.设点P的横坐标为m.
与x轴正半轴的交点,点B在这条抛物线上,且点B的横坐标为2.连接AB并延长交y轴于点C,抛物线的对称轴交AC于点D,交x轴于点E.点P在线段CA上,过点P作x轴的垂线,垂足为点M,交抛物线于点Q.设点P的横坐标为m.
(1)求直线AB对应的函数解析式.
(2)当四边形DEMQ为矩形时,求点Q的坐标.
(3)设线段PQ的长为d(d>0),求d关于m的函数解析式.
(4)在(3)的情况下,请直接写出当d随着m的增大而减小时,m的取值范围.
解:(1)令y=0,则- x2+5x=0,
x2+5x=0,
解得x1=0,x2=8,
∴点A的坐标为(8,0),
∵点B的横坐标为2,
∴y=- ×22+5×2=
×22+5×2= ,
,
∴点B的坐标为(2, ),
),
设直线AB的解析式为y=kx+b,
则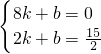 ,
,
解得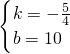 ,
,
∴直线AB的解析式为y=- x+10;
x+10;
(2)抛物线y=- x2+5x的对称轴为直线x=-
x2+5x的对称轴为直线x=-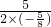 =4,
=4,
x=4时,y=- ×4+10=5,
×4+10=5,
∴DE=5,
∵四边形DEMQ为矩形,
∴MQ=5,即点Q的纵坐标为5,
∴- x2+5x=5,
x2+5x=5,
整理得,x2-8x+8=0,
解得x1=4-2 ,x2=4+2
,x2=4+2 (舍去),
(舍去),
∴点Q的坐标为(4-2 ,5);
,5);
(3)∵点P的横坐标为m,PM⊥x轴交抛物线于点Q,
∴点P(m,- m+10),点Q(m,-
m+10),点Q(m,- m2+5m),
m2+5m),
①点P在线段CB上时,线段PQ的长为d=(- m+10)-(-
m+10)-(- m2+5m)=
m2+5m)= m2-
m2- m+10,
m+10,
即d= m2-
m2- m+10;
m+10;
②点P在线段AB上时,线段PQ的长为d=(- m2+5m)-(-
m2+5m)-(- m+10)=-
m+10)=- m2+
m2+ m-10,
m-10,
即d=- m2+
m2+ m-10,
m-10,
∴d与m的关系式为d= ;
;
(4)①点P在线段CB上时,函数d= m2-
m2- m+10的对称轴为直线m=-
m+10的对称轴为直线m=- =5,
=5,
∵ >0,
>0,
∴d<5时,d随着m的增大而减小,
∵点P在线段CB上,
∴0<d<2,
②点P在线段AB上时,函数d=- m2+
m2+ m-10的对称轴为直线m=-
m-10的对称轴为直线m=-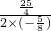 =5,
=5,
∵- <0,
<0,
∴d>5时,d随着m的增大而减小,
∵点P在线段AB上,
∴5<d<8,
综上所述,d随着m的增大而减小时,m的取值范围是0<d<2或5<d<8.
分析:(1)令y=0,解关于x的一元二次方程求出点A的坐标,再把x=2代入抛物线求出点B的坐标,然后设直线AB的解析式为y=kx+b,利用待定系数法求一次函数解析式解答即可;
(2)根据抛物线解析式求出对称轴,然后求出点D的坐标,得到DE的长度,再根据矩形的对边相等求出点Q的纵坐标然后代入抛物线解析式求出横坐标,即可得解;
(3)分点P在线段CB上和在线段AB上两种情况,用点P的纵坐标和点Q的纵坐标表示出PQ的长度,列式整理即可;
(4)分别求出二次函数图象的对称轴,然后利用二次函数的增减性解答.
点评:本题是二次函数综合题型,主要考查了抛物线与坐标轴交点的求法,待定系数法求一次函数解析式,垂直于坐标轴的两点间的距离的表示,以及二次函数的增减性,(3)(4)两个小题注意要根据点P的位置分情况讨论.
 x2+5x=0,
x2+5x=0,解得x1=0,x2=8,
∴点A的坐标为(8,0),
∵点B的横坐标为2,
∴y=-
 ×22+5×2=
×22+5×2= ,
,∴点B的坐标为(2,
 ),
),设直线AB的解析式为y=kx+b,
则
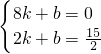 ,
,解得
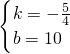 ,
,∴直线AB的解析式为y=-
 x+10;
x+10;(2)抛物线y=-
 x2+5x的对称轴为直线x=-
x2+5x的对称轴为直线x=-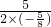 =4,
=4,x=4时,y=-
 ×4+10=5,
×4+10=5,∴DE=5,
∵四边形DEMQ为矩形,
∴MQ=5,即点Q的纵坐标为5,
∴-
 x2+5x=5,
x2+5x=5,整理得,x2-8x+8=0,
解得x1=4-2
 ,x2=4+2
,x2=4+2 (舍去),
(舍去),∴点Q的坐标为(4-2
 ,5);
,5);(3)∵点P的横坐标为m,PM⊥x轴交抛物线于点Q,
∴点P(m,-
 m+10),点Q(m,-
m+10),点Q(m,- m2+5m),
m2+5m),①点P在线段CB上时,线段PQ的长为d=(-
 m+10)-(-
m+10)-(- m2+5m)=
m2+5m)= m2-
m2- m+10,
m+10,即d=
 m2-
m2- m+10;
m+10;②点P在线段AB上时,线段PQ的长为d=(-
 m2+5m)-(-
m2+5m)-(- m+10)=-
m+10)=- m2+
m2+ m-10,
m-10,即d=-
 m2+
m2+ m-10,
m-10,∴d与m的关系式为d=
 ;
;(4)①点P在线段CB上时,函数d=
 m2-
m2- m+10的对称轴为直线m=-
m+10的对称轴为直线m=- =5,
=5,∵
 >0,
>0,∴d<5时,d随着m的增大而减小,
∵点P在线段CB上,
∴0<d<2,
②点P在线段AB上时,函数d=-
 m2+
m2+ m-10的对称轴为直线m=-
m-10的对称轴为直线m=-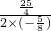 =5,
=5,∵-
 <0,
<0,∴d>5时,d随着m的增大而减小,
∵点P在线段AB上,
∴5<d<8,
综上所述,d随着m的增大而减小时,m的取值范围是0<d<2或5<d<8.
分析:(1)令y=0,解关于x的一元二次方程求出点A的坐标,再把x=2代入抛物线求出点B的坐标,然后设直线AB的解析式为y=kx+b,利用待定系数法求一次函数解析式解答即可;
(2)根据抛物线解析式求出对称轴,然后求出点D的坐标,得到DE的长度,再根据矩形的对边相等求出点Q的纵坐标然后代入抛物线解析式求出横坐标,即可得解;
(3)分点P在线段CB上和在线段AB上两种情况,用点P的纵坐标和点Q的纵坐标表示出PQ的长度,列式整理即可;
(4)分别求出二次函数图象的对称轴,然后利用二次函数的增减性解答.
点评:本题是二次函数综合题型,主要考查了抛物线与坐标轴交点的求法,待定系数法求一次函数解析式,垂直于坐标轴的两点间的距离的表示,以及二次函数的增减性,(3)(4)两个小题注意要根据点P的位置分情况讨论.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图,点P是抛物线y=x2上位于第一象限内一点,点A(3,0),设点P的坐标为(x,y).
如图,点P是抛物线y=x2上位于第一象限内一点,点A(3,0),设点P的坐标为(x,y). 的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点
的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点 ,则
,则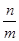 的值是 .
的值是 . 
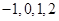 的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中取出一张,将卡片上的数字记为
的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中取出一张,将卡片上的数字记为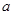 ,不放回,再取出一张,将卡片上的数字记为
,不放回,再取出一张,将卡片上的数字记为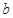 ,设
,设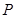 点的坐标为
点的坐标为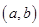 。如图,点
。如图,点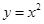 与直线
与直线 所围成的封闭区域内(图中含边界的阴影部分)的概率是
。
所围成的封闭区域内(图中含边界的阴影部分)的概率是
。
 的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点
的顶点,点A1、A2都在该抛物线上,四边形OA1B1C1、OA2B2C2均为正方形,点B2在y轴上,直线C2B2与该抛物线交于点 ,则
,则 的值是 .
的值是 .
