题目内容
探索:先观察并计算下列各式,在空白处填上“>,<,=”,并完成式后的问题.
(1)22+32 2×2×3,42+52 2×4×5,
72+72 2×7×7,52+82 2×5×8,…
试用含有a,b的式子表示上述规律为
(2)(1+2+3)2 3×1×2×3,(2+3+5)2 3×2×3×5,
(4+4+7)2 3×4×4×7,(5+5+5)2 3×5×5×5,…
试用含有a,b,c的式子表示上述规律为 .
(1)22+32
72+72
试用含有a,b的式子表示上述规律为
(2)(1+2+3)2
(4+4+7)2
试用含有a,b,c的式子表示上述规律为
考点:规律型:数字的变化类
专题:规律型
分析:(1)先计算,再比较大小,进一步得出规律,用式子表示答案即可;
(2)先计算,再比较大小,进一步得出规律,分类用式子表示答案即可.
(2)先计算,再比较大小,进一步得出规律,分类用式子表示答案即可.
解答:解:(1)22+32>2×2×3,42+52>2×4×5,
72+72=2×7×7,52+82>2×5×8,…
用含有a,b的式子表示上述规律为:a2+b2≥2ab;
(2)(1+2+3)2>3×1×2×3,(2+3+5)2>3×2×3×5,
(4+4+7)2<3×4×4×7,(5+5+5)2<3×5×5×5,…
试用含有a,b,c(a≤b≤c)的式子表示上述规律为:
当a+b≤c时,(a+b+c)2>3abc,
当a+b>c时,(a+b+c)2<3abc.
故答案为:(1)>,>,=,>,a2+b2≥2ab;(2)>,>,<,<,当a+b≤c时,(a+b+c)2>3abc,当a+b>c时,(a+b+c)2<3abc.
72+72=2×7×7,52+82>2×5×8,…
用含有a,b的式子表示上述规律为:a2+b2≥2ab;
(2)(1+2+3)2>3×1×2×3,(2+3+5)2>3×2×3×5,
(4+4+7)2<3×4×4×7,(5+5+5)2<3×5×5×5,…
试用含有a,b,c(a≤b≤c)的式子表示上述规律为:
当a+b≤c时,(a+b+c)2>3abc,
当a+b>c时,(a+b+c)2<3abc.
故答案为:(1)>,>,=,>,a2+b2≥2ab;(2)>,>,<,<,当a+b≤c时,(a+b+c)2>3abc,当a+b>c时,(a+b+c)2<3abc.
点评:此题考查数字的运算规律,注意数字之间的联系,找出规律解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知关于x的不等式组
无解,则a的取值范围是( )
|
| A、a≤-1 |
| B、a≤2 |
| C、-1<a<2 |
| D、a<-1或a>2 |
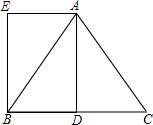 如图,在△ABC中,AB=AC,AD是BC边上的中线,四边形ADBE是平行四边形,求证:四边形ADBE是矩形.
如图,在△ABC中,AB=AC,AD是BC边上的中线,四边形ADBE是平行四边形,求证:四边形ADBE是矩形.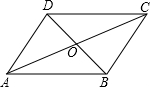 如图,在?ABCD中,对角线AC、BD相交于点O.如果AB=8,AC=14,BD=x,那么x的取值范围是
如图,在?ABCD中,对角线AC、BD相交于点O.如果AB=8,AC=14,BD=x,那么x的取值范围是