题目内容
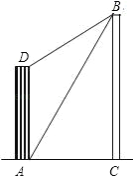
【题目】大楼AD的高为10米，不远处有一塔BC，某人在楼底A处测得塔顶B处的仰角为60°，爬到楼顶D点测得塔顶B点的仰角为30°，求塔BC的高度．
【答案】15米.
【解析】
试题分析：过点B作BE⊥AD交AD延长线于点E，构造两个直角三角形．设DE=x，分别求解可得AD与DE的值，再利用BC=AD+DE，即可求出答案．
试题解析：过点B作BE⊥AD，交AD延长线于点E．
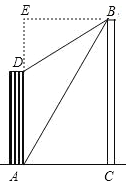
在Rt△BED中，∵D点测得塔顶B点的仰角为30°，
∴∠BDE=60度．
设DE=x，则BE=
x．
在Rt△BEA中，∠BAE=30度，BE=x．
∴AE=3x．
∴AD=AE-DE=3x-x=2x=10．
∴x=5．
∴BC=AD+DE=10+5=15（米）．
答：塔BC的高度为15米．
练习册系列答案
阅读快车系列答案
相关题目
