Question

如图①，P是线段AB上一点，△APC与△BPD是等边三角形（三边相等，三个角都为60°的三角形）．
（1）请你判断：AD与BC相等吗？并说明理由；
（2）如图②，若△BPD绕P点旋转一定角度，（1）中的结论还成立吗？

Answer 1

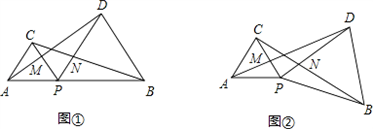
解：（1）AD=BC，理由：
∵△APC和△BPD都是等边三角形
∴∠APC=∠DPB=∠CPD=60°
∴∠APC+∠CPD=∠DPB+∠CPD
在△APC和△BPD中
∵AP=CP，∠APD=∠CPB，DP=BP
∴△APC≌△BPD（SAS）
∴AD=BC（全等三角形对应边相等）
（2）条件改变，结论仍然成立．
∵△APC和△BPD都是等边三角形
∴∠APC=∠DPB=∠CPD=60°
∴∠APC+∠CPD=∠DPB+∠CPD
∴∠APD=∠CPB
在△APC和△BPD中
∵AP=CP，∠APD=∠CPB，DP=BP
∴△APC≌△BPD（SAS）
∴AD=BC（全等三角形对应边相等）