题目内容
【题目】若平面直角坐标系中的点作如下平移：沿x轴方向平移的数量为a（向右为正，向左为负，平移|a|个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移|b|个单位），则把有序数对{a，b}叫做这一平移的“平移量”．规定“平移量”{a，b}与“平移量”{c，d}的加法运算法则为{a，b}+{c，d}={a+c，b+d}．
（1）若动点P从坐标点M（1，1）出发，按照“平移量”{2，0}平移到N，再按照“平移量”{1，2}平移到G，形成△MNG，则点N的坐标为 ， 点G的坐标为 ．
（2）若动点P从坐标原点出发，先按照“平移量”m平移到B，再按照“平移量”n平移到C；最后按照“平移量”q平移回到点O．当△OBC∽△MNG（在（1）中的三角形）．且相似比为2：1时，请你直接写出“平移量”m ， n ， q ．
（3）在（1）、（2）的前提下，请你在平面直角坐标系中画出△OBC与△MNG．
【答案】
（1）（3，1）；（4，3）
（2）{4，0}或{4，0}或{﹣4，0}或{﹣4，0}；{2，4}或{2，﹣4}或{﹣2，4}或{2，4}；{﹣6，﹣4}或{﹣6，4}或{6，4}或{6，﹣4}
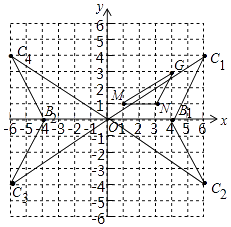
（3）
解：如图所示△OB1C1，△OB1C2，△OB2C3，△OB2C4都满足条件．
【解析】解：（1）动点P从坐标点M（1，1）出发，按照“平移量”{2，0}平移到N，再按照“平移量”{1，2}平移到G，形成△MNG，则点N的坐标为 （3，1），点G的坐标为 （4，3），所以答案是（3，1），（4，3）．
（2）△OBC∽△MNG（在（1）中的三角形）．且相似比为2：1时，①当△OB1C1∽△MNG时，m{4，0}，n{2，4}，q{﹣6，﹣4}，②当△OB1C2∽△MNG时，m{4，0}，n{2，﹣4}，q{﹣6，4}，③当△OB2C3∽△MNG时，m{﹣4，0}，n{﹣2，4}，q{6，4}，④当△OB2C4∽△MNG时，m{﹣4，0}，n{2，4}，q{6，﹣4}，所以答案是{4，0}或{4，0}或{﹣4，0}或{﹣4，0}；{2，4}或{2，﹣4}或{﹣2，4}或{2，4}；{﹣6，﹣4}或{﹣6，4}或{6，4}或{6，﹣4}．
【考点精析】解答此题的关键在于理解平移的性质的相关知识，掌握①经过平移之后的图形与原来的图形的对应线段平行（或在同一直线上）且相等，对应角相等，图形的形状与大小都没有发生变化；②经过平移后，对应点所连的线段平行（或在同一直线上）且相等，以及对相似三角形的性质的理解，了解对应角相等，对应边成比例的两个三角形叫做相似三角形．
