题目内容
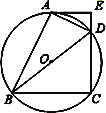
【题目】如图,已知等边三角形![]() 的边长为
的边长为![]() ,点
,点![]() 为平面内一动点,且
为平面内一动点,且![]() ,将点
,将点![]() 绕点
绕点![]() 按逆时针方向转转
按逆时针方向转转![]() ,得到点
,得到点![]() ,连接
,连接![]() ,则
,则![]() 的最大值__________.
的最大值__________.
【答案】![]() +1.
+1.
【解析】
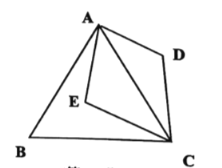
如图,连接BE,易证△BCE≌△ACD,从而证得BE=AD=1.再由AE≤AB+BE,当E点在AB的延长线上时AE取得最大值.
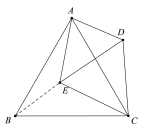
解:如图所示,连接BE,
∵△ABC是等边三角形,
∴AB=BC=AC= ![]() ,∠ACB=60°.
,∠ACB=60°.
∵将点![]() 绕点
绕点![]() 按逆时针方向转转
按逆时针方向转转![]() ,得到点
,得到点![]() ,
,
∴EC=DC, ∠DCE=60°.
∴∠ACB=∠DCE.
∴∠ACB-∠ACE=∠DCE-∠ACE.
即:∠ACD=∠BCE.
在△BCE和△ACD中,
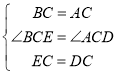 ,
,
∴△BCE≌△ACD,
∴BE=AD=1.
在△ABE中,
∵AE≤AB+BE.
∴当点E在AB的延长线上时,AE有最大值,最大值为![]() +1.
+1.
故答案为:![]() +1.
+1.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目