题目内容
【题目】如图,在△ABC中,AB=AC=4,BD是△ABC的中线,∠ADB=120°,点E在中线BD的延长线上,则△ACE是直角三角形时,DE的长为 . 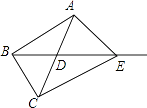
【答案】2或4
【解析】解:△ACE为直角三角形分三种情况: ①当∠CAE=90°时,
∵∠ADB=120°,
∴∠ADE=60°,∠AED=30°.
∵AB=AC=4,BD是△ABC的中线,
∴AD=CD=2.
∴DE= ![]() =
= ![]() =4;
=4;
②当∠AEC=90°时,
∵ED是△EAC的中线,
∴DE= ![]() AC=2;
AC=2;
③当∠ACE=90°时,
∵∠ADB=120°,
∴∠CDE=60°,∠CED=30°.
∵AB=AC=4,BD是△ABC的中线,
∴AD=CD=2.
∴DE= ![]() =
= ![]() =4.
=4.
综上可知:DE的长为2或4.
所以答案是:2或4.
【考点精析】利用等腰三角形的性质和含30度角的直角三角形对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目