Question

如图，直线y＝2x＋2与y轴交于A点，与反比例函数y＝(x＞0)的图象交于点M，过M作MH⊥x轴于点H，且tan∠AHO＝2．

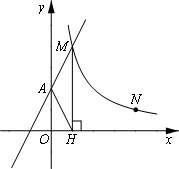
(1)求k的值；

(2)点N(a，1)是反比例函数y＝(x＞0)图像上的点，在x轴上是否存在点P，使得PM＋PN最小，若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

答案：
解析：

解：(1)由y＝2x＋2可知A(0，2)，即OA＝2．(1分) 　　∵tan∠AHO＝2，∴OH＝1．(2分) 　　∵MH⊥x轴，∴点M的横坐标为1． 　　∵点M在直线y＝2x＋2上， 　　∴点M的纵坐标为4．即M(1，4)．(3分) 　　∵点M在y＝上，∴k＝1×4＝4．(4分) 　　(2)∵点N(a，1)在反比例函数(x＞0)上， 　　∴a＝4．即点N的坐标为(4，1)．(5分) 　　过N作N关于x轴的对称点N1，连接MN1，交x轴于P(如图)． 　　此时PM＋PN最小．(6分) 　　∵N与N1关于x轴的对称，N点坐标为(4，1)， 　　∴N1的坐标为(4，－1)．(7分) 　　设直线MN1的解析式为y＝kx＋b． 　　由 　　解得k＝－，b＝．(9分) 　　∴直线MN1的解析式为． 　　令y＝0，得x＝． 　　∴P点坐标为(，0)．(10分)